Archivi categoria: Matematica

Post di matematica

Ellisse: dimostrazione geometrica dell’equivalenza delle sue due definizioni

“Ogni volta che cerco di approfondire la teoria della gravitazione di Newton mi imbatto, prima o poi, nell’ellisse e nelle sue proprietà geometriche.
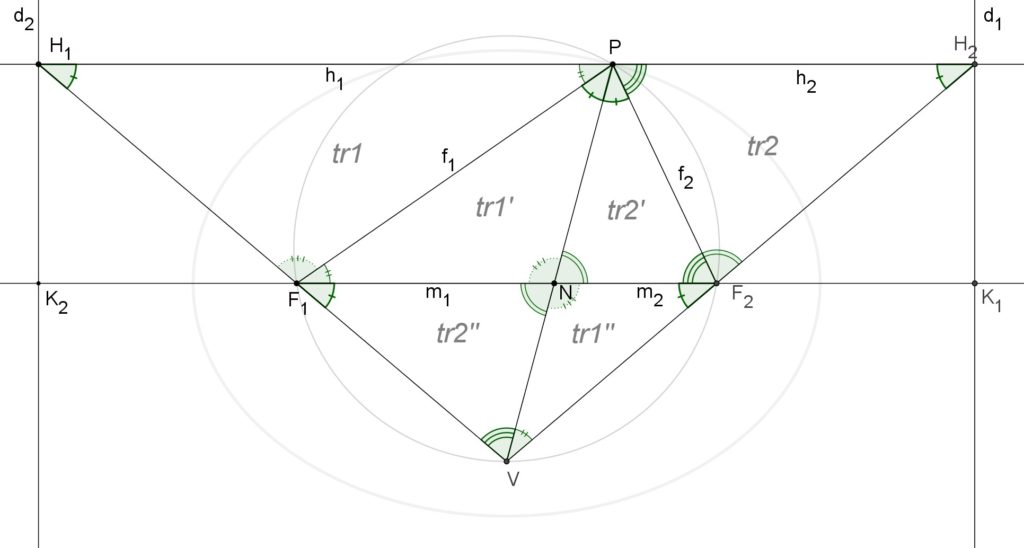
Dopo diversi anni sono sempre più convinto che raggiungere una migliore comprensione dell’ellisse e delle sue numerose proprietà geometriche, anche le più sottili e nascoste, sia un passaggio fondamentale per capire più a fondo le teorie fisiche e matematiche in cui essa compare.

La definizione geometrica dell’ellisse può essere formulata tramite due definizioni alternative ma equivalenti…“

Ellipse construction from focus-directrix[vai alla pagina]

Il problema del lancio di dadi con una data somma

Qualche esercizio di calcolo combinatorio può proporre domande del tipo: “se si lanciano due dadi qual’è la la probabilità che la somma dei numeri delle due facce sia 9?”
La risposta non è particolarmente difficile se si enumerano i casi che soddisfano il particolare evento richiesto (somma=9), dividendo poi tale numero di “eventi favorevoli” per il numero dei “casi possibili“.
Ma come affrontare lo stesso tipo di problema se si vuole calcolare la probabilità, ad esempio, di ottenere la somma 31 lanciando 10 dadi? In questo caso il conteggio dei casi favorevoli per enumerazione richiederebbe un tempo davvero molto lungo!
In casi come quest’ultimo è possibile ricavare una formula generale che fornisca la probabilità di avere una qualsiasi somma (p) lanciando un qualsiasi numero (n) di dadi?

Leggi l’articolo completo…

Pioggia

A volte la matematica può essere totalmente inutile, ma sorprendentemente semplice e bella…

Un altro esempio è la seguente animazione, che è stata generata in Wolfram Mathematica tramite un codice davvero molto breve (solo 221 caratteri di lunghezza):

Animate[With[{r := RandomReal[]}, 
  Graphics[BlockRandom[
    Table[With[{z = r}, {, GrayLevel[2 (t - z)], 
       Thickness[0.03 (0.20 - t + z)], 
       Circle[{1.7 r, 0.82 r}, Max[0, t - z]]}], {k, 1, 45}]], 
   PlotRange -> {{0, 1.7}, {0, 0.82}}]],
{t, 0, 1}, DefaultDuration -> 20]

Troppo per poter essere inviata al twitter @wolframtap (Wolfram Tweet-a-Program). Ma abbastanza breve da mostrare come alcune semplici idee matematiche possono essere davvero molto semplici e belle (anche se, forse, inutili). Ecco il video inviato a youtube:

Una “specie” di torre Eiffel (quando la matematica è inutile ma bella)

A volte la matematica può essere totalmente inutile, ma sorprendentemente semplice e bella.
Un possibile esempio di questa idea è la seguente immagine, che si può generare, in Wolfram Mathematica, con un codice di lunghezza inferiore a quello di un twit (123 caratteri):

Graphics3D[Table[Rotate[Cuboid[{-0.9^k, -0.9^k, (1/20)*k}, 
{0.9^k, 0.9^k, (1/20)*(k + 1)}], k*0.1, {0, 0, 1}], {k, 0, 60}]]

EiffelQuesto mini-programma è stato anche pubblicato nel twitter @wolframtap (Wolfram Tweet-a-Program).

QUI il collegamento al twit.

Un altro interessante aspetto relativo al fantasioso e stravagante edificio rappresentato nell’immagine è il fatto che, malgrado esso possa avere un’altezza infinita, avrà comunque un volume finito.

In questa pagina è presentata una versione un poco più estesa del programma, con una dimostrazione interattiva in cui è possibile modificare l’angolo tra parallelepipedi consecutivi.

(Grazie a BV per avermi suggerito questa idea)

Propagazione delle onde nello spazio e nel tempo

Non è facile comprendere gli aspetti matematici del moto di un’onda.
Il fatto è che un’onda è una perturbazione (in un mezzo) che cambia nello spazio e nel tempo.
Quindi, anche nel più semplice dei casi (ad esempio quello di un’onda che si propaga in un mezzo a 1 dimensione, come una corda) ci sono almeno 3 variabili coinvolte: il grado di perturbazione del mezzo, la posizione e il tempo.

Per capire meglio le relazioni tra queste variabili e i parametri dell’onda ho pensato di creare, con il programma Wolfram Mathematica una dimostrazione interattiva sulle onde.
La dimostrazione è stata esportata nel formato .cdf in modo da poter essere utilizzata con il programma gratuito CDF Player (si veda la pagina “Come utilizzare le dimostrazioni CDF” per informazioni sull’installazione).

La dimostrazione CDF (con ulteriori spiegazioni) è disponibile in questa pagina.

Nella simulazione sono mostrati 4 diversi grafici:

• L’onda che si propaga nella direzione x
• Il profilo temporale dell’onda in una posizione predefinita x_0
• Il profilo spaziale dell’onda, catturato in istanti particolari (evidenziati dall’effetto “flash“)
• La vista 3D, che unisce la variabile spaziale e quella temporale e in cui è anche visualizzato un punto mobile che rappresenta lo stato della perturbazione (direzione verticale) nella posizione x_0 al passare del tempo e la sua traiettoria spazio-temporale.

Nella dimostrazione è possibile modificare i parametri dell’onda e vedere i relativi cambiamenti nella sua evoluzione spazio-temporale.
Chi non ha installato il CDF Player sul proprio PC (o chi accede a questo sito tramite smartphone/tablet iOS/Android) può avere un’idea della simulazione tramite questo breve video dimostrativo:

La matematica dei social network e la teoria dei “sei gradi di separazione”

Da: http://it.wikipedia.org/wiki/Sei_gradi_di_separazione

“La teoria dei sei gradi di separazione in semiotica e in sociologia è un’ipotesi secondo cui qualunque persona può essere collegata a qualunque altra persona o cosa attraverso una catena di conoscenze e relazioni con non più di 5 intermediari“

Tale teoria mi ha spesso incuriosito e, recentemente, mi sono dedicato ad investigare i suoi fondamenti matematici.

Tale ricerca è anche stata stimolata dalla lettura dei seguenti testi (in inglese):

  • Duncan J. Watts – Small Worlds: The Dynamics of Networks between Order and Randomness –  Princeton University Press – 1999
  • Steven Strogatz – Sync – Penguin Books – 2003

Come primo passo ho esaminato alcuni dei modelli matematici (descritti nei testi citati) in grado di riprodurre i meccanismi essenziali che regolano il processo dinamico di interconnessione tra le persone (o tra altri elementi di una rete).
I primi risultati di questa personale ricerca sono riportati nella seguente pagina, che contiene anche una simulazione interattiva sul modello α di Duncan Watts. Tale simulazione è stata realizzata con il software Mathematica e poi esportata come file utilizzabile dal CDF Player (il CDF player è scaricabile gratuitamente – vedi home page).

Vai alla pagina della dimostrazione

Vai alla pagina della dimostrazione (versione in inglese)