[nota: una versione inglese di questo articolo, con leggere differenze, è stata pubblicata su arXiv con il titolo ““The toric sections: a simple introduction” e può essere scaricata come pdf al link https://arxiv.org/pdf/1708.00803 o da questo sito (The toric sections: a simple introduction)]
Introduzione
La curva di intersezione tra un toro e un piano è chiamata sezione torica.
Anche se entrambe le superfici sono piuttosto semplici da definire e sono descritte da equazioni abbastanza semplici, la sezione torica ha una equazione abbastanza complessa e può assumere forme piuttosto interessanti.
In questo articolo verranno discusse alcune proprietà di questa curva evidenziando le sue differenze con le ben più famose sezioni coniche. Successivamente si mostrerà come costruire la sua equazione generale (quartica) e si noterà come la stessa curva possa anche essere generata dall’intersezione di un cilindro con un cono. Infine verranno presentate alcune brevi note sull’utilizzo del software Geogebra per visualizzare le diverse forme delle sezioni toriche nella finestra grafica 3D del programma.
L’articolo si basa in gran parte su procedimenti algebrici di base, senza richiedere quindi la conoscenza di strumenti matematici avanzati. Per seguire l’articolo è comunque necessario possedere qualche nozione di goniometria e di geometria analitica dello spazio.
Il toro e le sezioni toriche
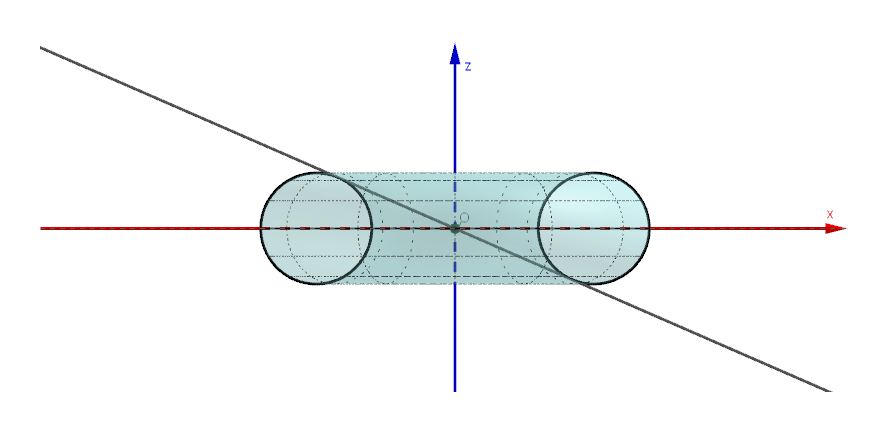
La superficie torica (fig. 10) è generata ruotando una circonferenza di raggio r attorno a un asse co-planare con la stessa circonferenza, sequendo una seconda circonferenza di raggio R. I due raggi r e R sono quindi i due parametri che determinano la forma del toro. Nelle righe seguenti assumeremo sempre (se non altrimenti specificato) che ![]() (in modo da evitare auto-intersezioni), e che, in un sistema di riferimento cartesiano, il piano equatoriale del toro sia il piano xy e l’asse di rotazione del toro sia l’asse z.
(in modo da evitare auto-intersezioni), e che, in un sistema di riferimento cartesiano, il piano equatoriale del toro sia il piano xy e l’asse di rotazione del toro sia l’asse z.
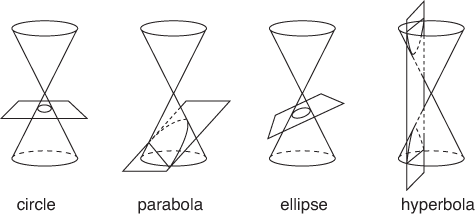
Una sezione torica è del tutto analoga a una sezione conica in quanto la prima rappresenta la curva di intersezione tra un toro e un piano mentre la seconda è la curva di intersezione tra una superficie conica e un piano.
Ma mentre le sezioni coniche hanno una (meritata) fama, anche per la loro ricorrente comparsa in molte importanti leggi della fisica classica, le sezioni toriche sono spesso confinate nell’ambito delle curiosità matematiche e delle curve esotiche. Eppure…
The variety of the toric sections is quite rich and the study of the case when sectioning planes are parallel to the symmetry axis of the torus dates back to antiquity. The corresponding curves are usually called “the spiric sections of Perseus” after their discoverer (circa 150 BC). Among them, one can distinguish Cassini’s curves (in particular, Bernoulli’s lemniscate).
[da: Sym, Antoni (2009), “Darboux’s greatest love”, J. Phys. A: Math. Theor. 42 (2009) 404001]
La “varietà” delle sezioni toriche
In questa sezione descriveremo e presenteremo alcuni particolari tipi di sezioni toriche che hanno una certa rilevanza storica. Tra queste troviamo i cerchi di Villarceau, gli ovali di Cassini, la lemniscata di Bernoulli e l’ippopede di Proclo.
La sezione torica centrale e i cerchi di Villarceau
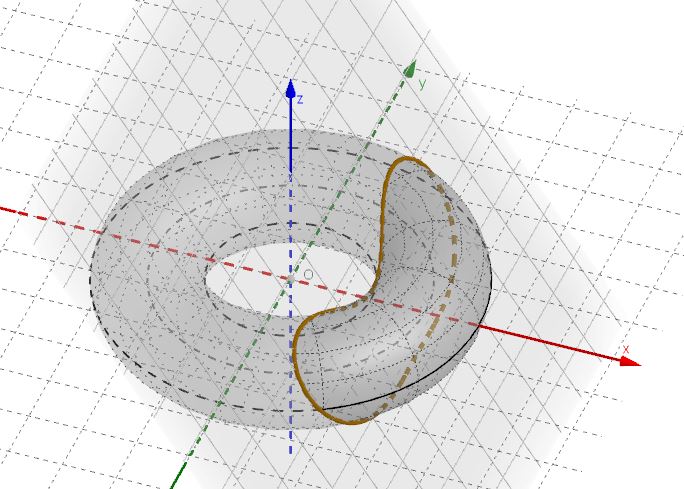
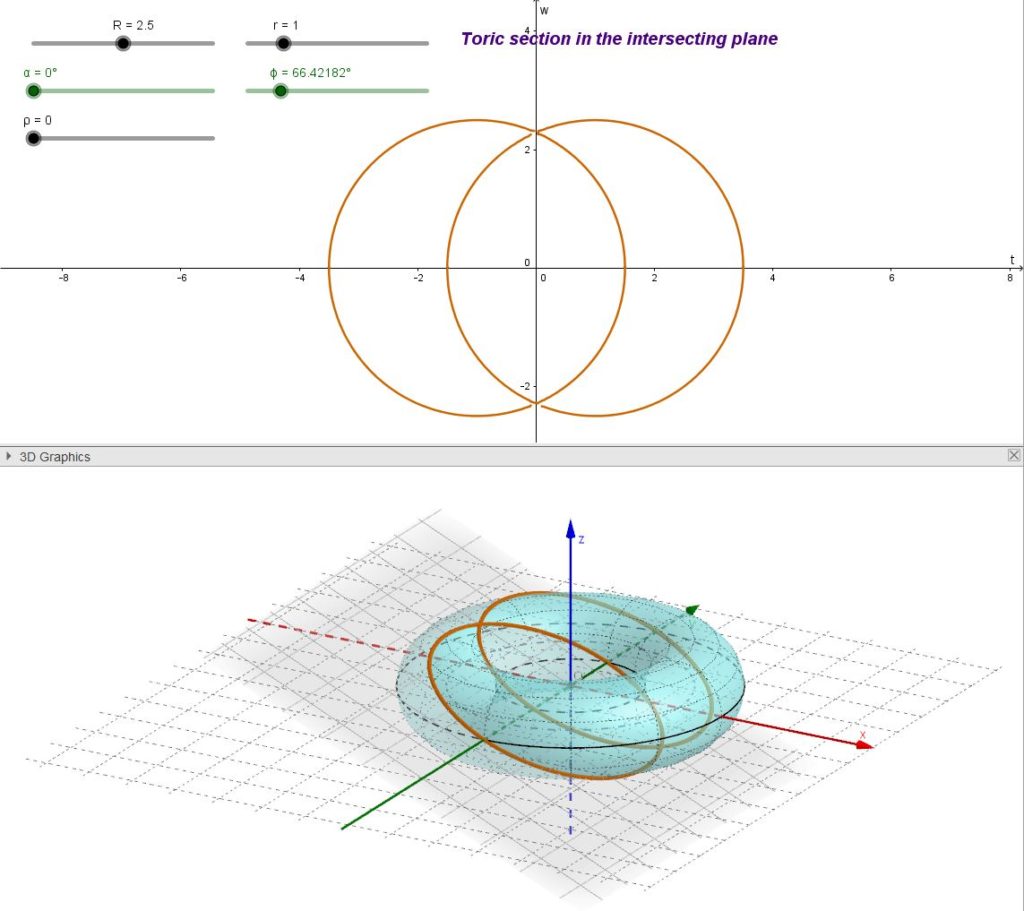
Una sezione torica in cui il piano intersecante passa dal centro del toro è chiamata sezione torica centrale.
Le sezioni toriche centrali possono essere circonferenze nei seguenti casi:
- il piano intersecante è il piano equatoriale
- il piano intersecante è perpendicolare al piano equatoriale
- il piano intersecante è (localmente) tangente alla superficie del toro in due punti isolati.
Nell’ultimo caso (il meno banale) la sezione torica è costituita da due circonferenze usualmente chiamate cerchi di Villarceau.
Sezioni toriche centrali – altre sezioni
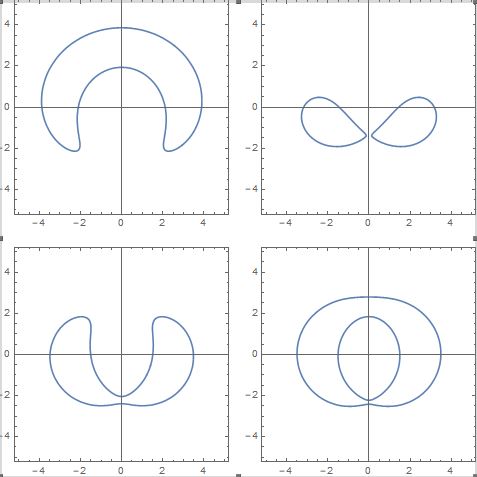
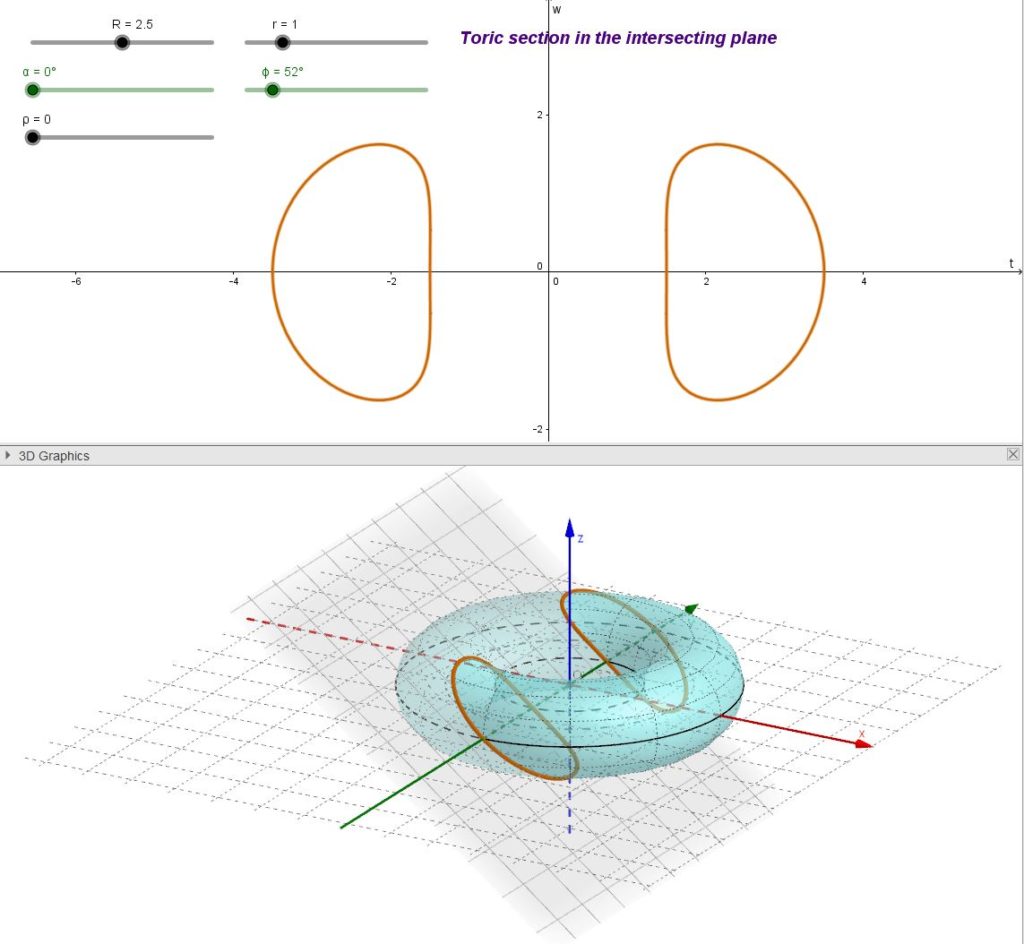
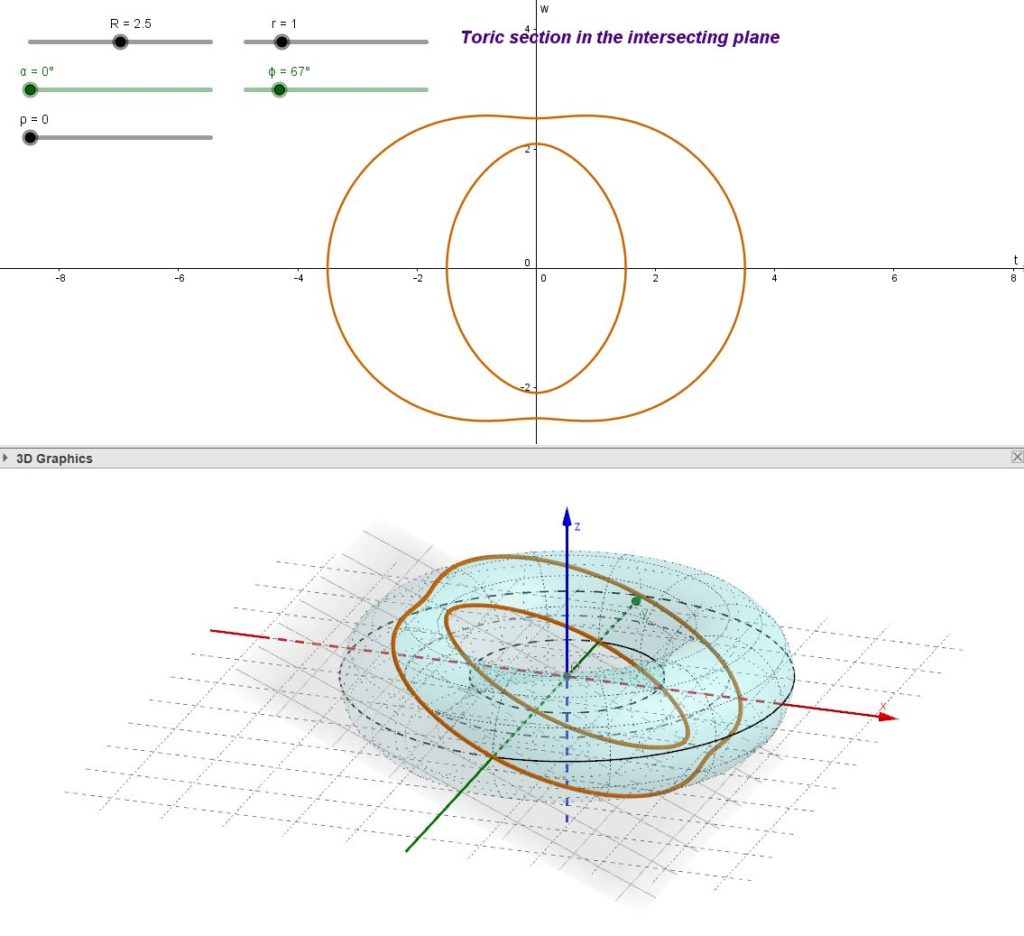
Osserviamo che, se alcune sezioni toriche centrali sono circonferenze questo non vuol dire che tutte le sezioni toriche centrali siano circonferenze, come mostrato nella figura seguente
 |
 |
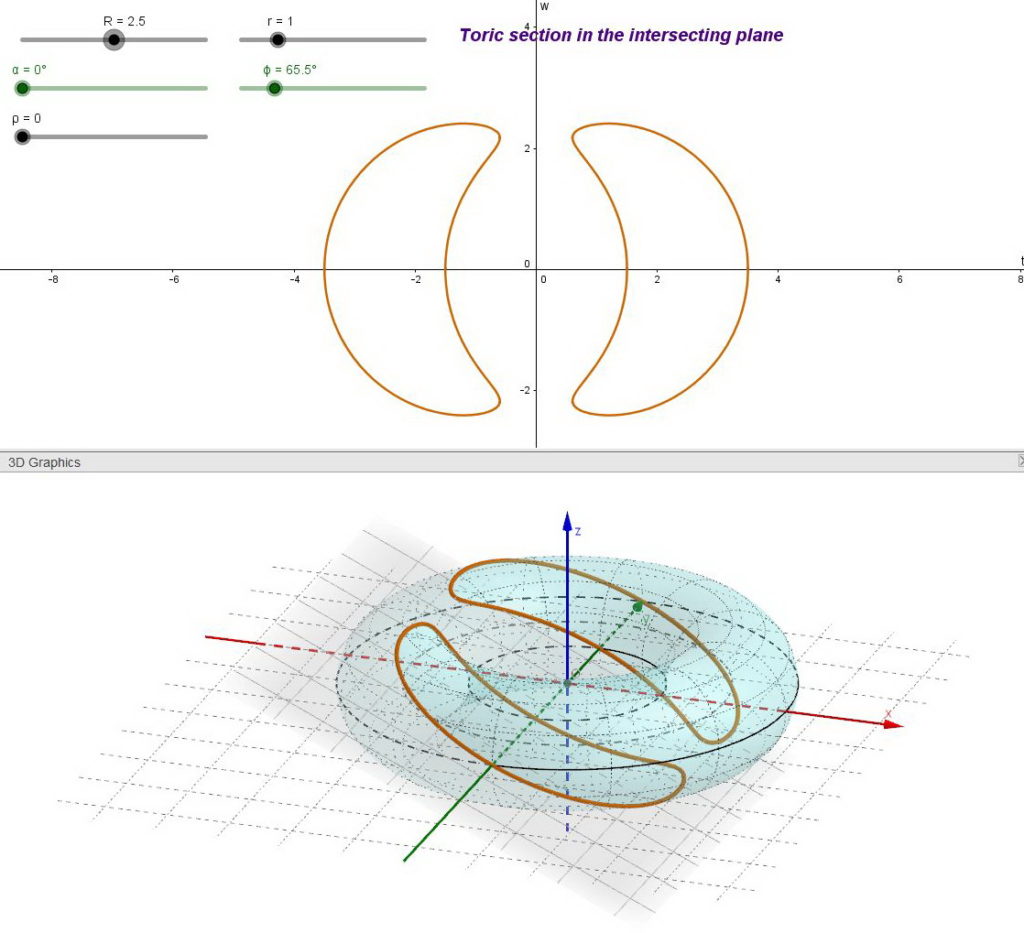 |
| fig. 04 – Alcune generiche sezioni toriche centrali |
||
Sezioni spiriche
Le sezioni torica generata da un piano intersecante parallelo all’asse rotazionale del toro (o, equivalentemente, perpendicolare al suo piano equatoriale) sono chiamate sezioni spiriche. Il nome deriva dalla parola “σπειρα” che significa “toro” in greco classico.
Rientrano in questa categoria gli ovali di Cassini e le lemniscate di Bernoulli.
Gli ovali di Cassini sono particolari sezioni spiriche in cui la distanza ![]() del piano secante dall’asse del toro eguaglia il raggio minore r del cerchio la cui rotazione genera la superficie del toro.
del piano secante dall’asse del toro eguaglia il raggio minore r del cerchio la cui rotazione genera la superficie del toro.
Una interessante definizione alternativa di un ovale di Cassini è quella del luogo dei punti P tali che il prodotto delle loro distanze da due punti fissi F1 and F2 sia costante:
![]()
Questa definizione richiama quella dell’ellisse, ma in questo caso si considera il prodotto al posto della somma.
Se la distanza focale è ![]() , i parametri degli ovali di Cassini, con riferimento al toro intersecato, sono
, i parametri degli ovali di Cassini, con riferimento al toro intersecato, sono ![]() and
and ![]() .
.
 |
 |
| fig. 05 – Due diversi esempi di ovali di Cassini | |
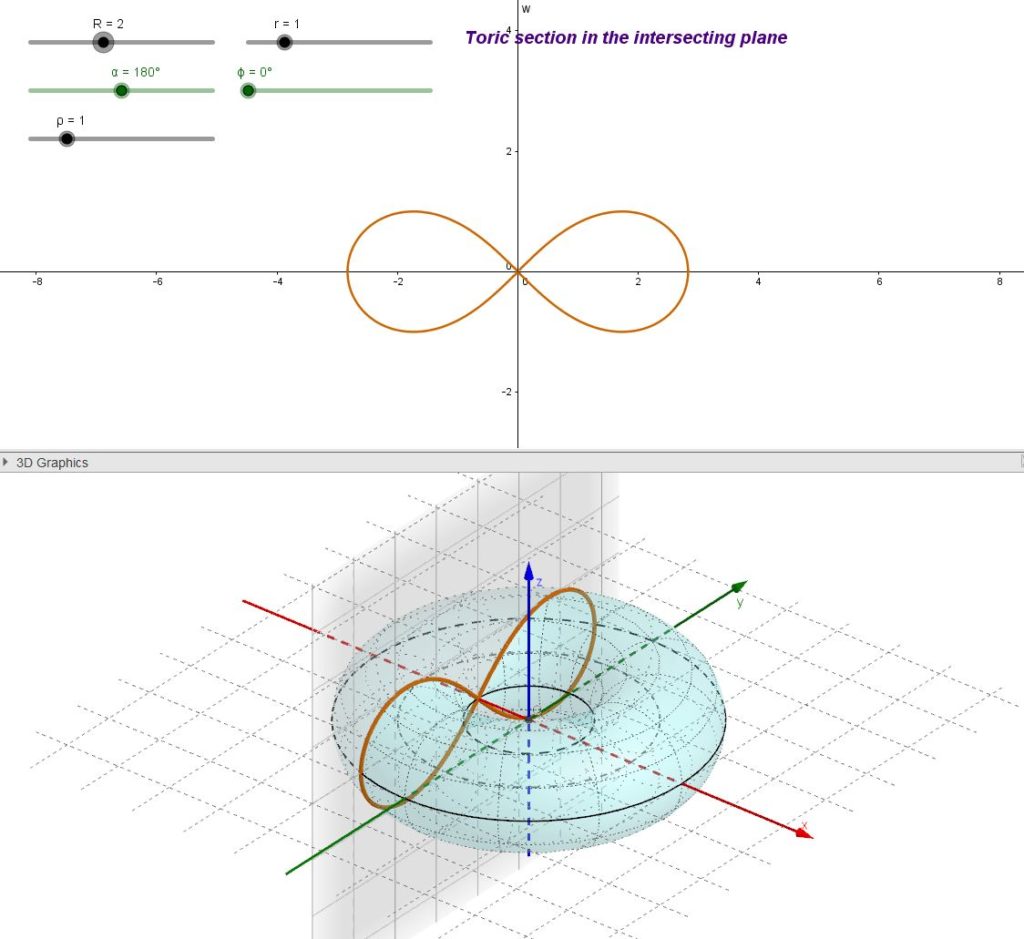
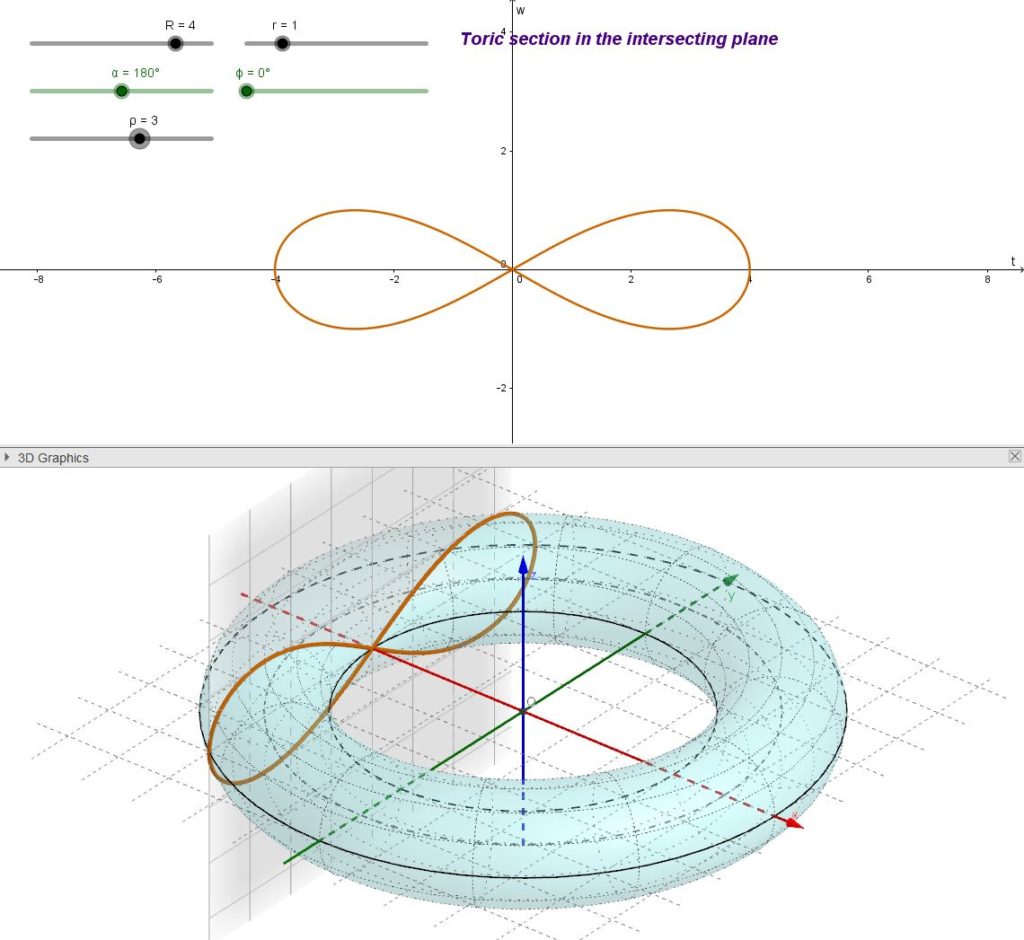
La lemniscata di Bernoulli è, a sua volta, un caso particolare di ovale di Cassini. Infatti è generata come un ovale di Cassini con l’ulteriore imposizione che sia ![]() . In pratica il piano secante deve essere tangente all’equatore interno del toro.
. In pratica il piano secante deve essere tangente all’equatore interno del toro.
La lemniscata di Bernoulli può anche essere definita come il luogo dei punti P tali che il prodotto delle loro distanze da due punti fissi F1 and F2 sia costante e sia anche uguale al quadrato della semidistanza focale:
![]() dove
dove ![]() .
.
Come curiosità possiamo osservare che questa curva lemniscata, che assomiglia a un “otto” ruotato di 90°, è stata utilizzata, a partire dal XVII secolo, come simbolo dell’infinito matematico (sembra che la prima apparenza di questo simbolo nel suo attuale significato di infinito matematico sia avvenuta nel trattato “De sectionibus conicis” di John Wallis nel 1655).
Se si rilascia il vincolo ![]() che caratterizza gli ovali di Cassini ma si mantiene la condizione di tangenza del piano intersecante all’equatore interiore (dovrà quindi essere
che caratterizza gli ovali di Cassini ma si mantiene la condizione di tangenza del piano intersecante all’equatore interiore (dovrà quindi essere ![]() ) si ottiene una nuova famiglia di curve chiamate Ippopede di Proclo.
) si ottiene una nuova famiglia di curve chiamate Ippopede di Proclo.
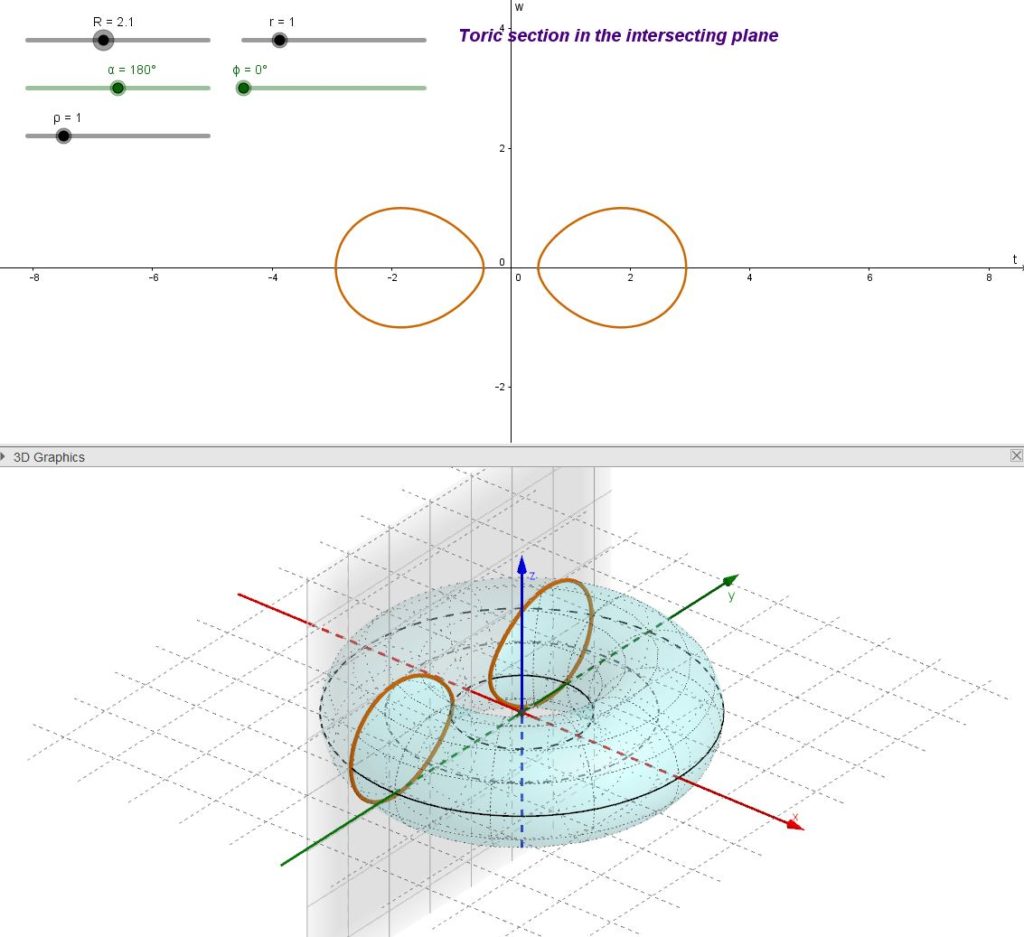
Sezioni toriche generiche
Esistono altre sezioni toriche che non sono nè sezione centrali nè sezioni spiriche. In queste il piano secante avrà una certa generica inclinazione rispetto al piano equatoriale e non passerà per il centro del toro. Ecco qualche esempio:
Sezioni toriche e sezioni coniche
Il toro è generato dalla rotazione di una circonferenza attorno a un asse coplanare con la circonferenza stessa. In altre parole è prodotto dalla rotazione attorno a una prima circonferenza di centro O di una seconda circonferenza di centro O’, mantenendo il piano di quest’ultima perpendicolare alla tangente alla prima circonferenza in O’ (fig. 10).
Dall’altra parte una superfice conica (intendiamo qui una superficie conica circolare retta) è generata ruotando una retta attorno a un’altra retta intersecante la prima mantenendo costante l’angolo tra le due rette (fig. 09).
La principale differenza tra le due superfici può quindi essere ricondotta al confronto tra le definizioni sintetiche “circonferenza ruotata attorno a una retta” in opposizione a “retta ruotata attorno a una retta“.
Dato che in un sistema di riferimento cartesiano la circonferenza è rappresentata da una equazione di secondo grado nelle coordinate x e y e una retta da una equazione di primo grado e dato che la rotazione attorno a un asse implica un secondo percorso di tipo circolare, si può cominciare a intuire che l’equazione di un toro (e di una sezione torica) sarà di quarto grado mentre l’equazione di una superficie conica (e di una sezione conica) sarà di secondo grado. Tale intuizione, basata su un ragionamento molto qualitativo e astratto, tutto da verificare, si rivelerà corretta.
L’equazione della superficie conica e quella del toro
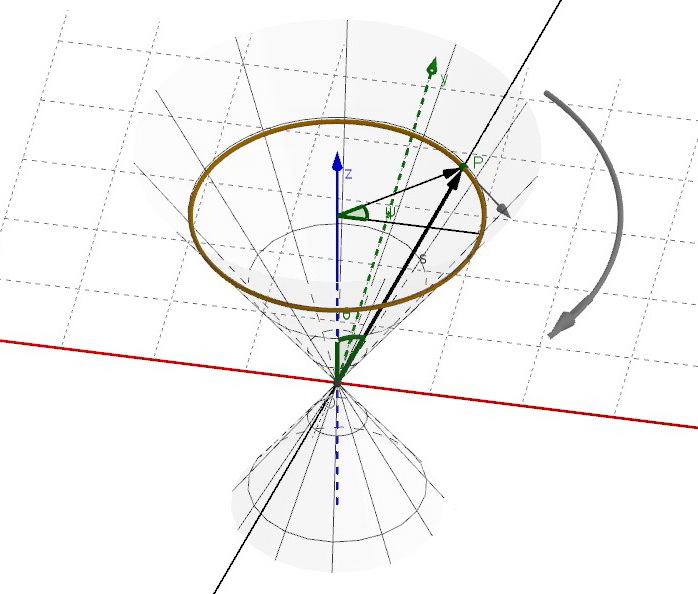
Una superficie conica circolare retta di apertura ![]() , con asse di rotazione l’asse
, con asse di rotazione l’asse ![]() e con vertice nell’origine O, è descritta dalle equazioni parametriche
e con vertice nell’origine O, è descritta dalle equazioni parametriche
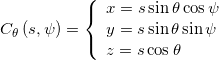
dove, se P è un punto sulla superficie, il parametro s è la coordinata di P lungo la retta orientata OP e il parametro ![]() è l’angolo di rotazione di P attorno all’asse z.
è l’angolo di rotazione di P attorno all’asse z.
La figura seguente mostra il significato delle equazioni parametriche sopra riportate.
In coordinate cartesiane la superficie conica ha equazione
![]()
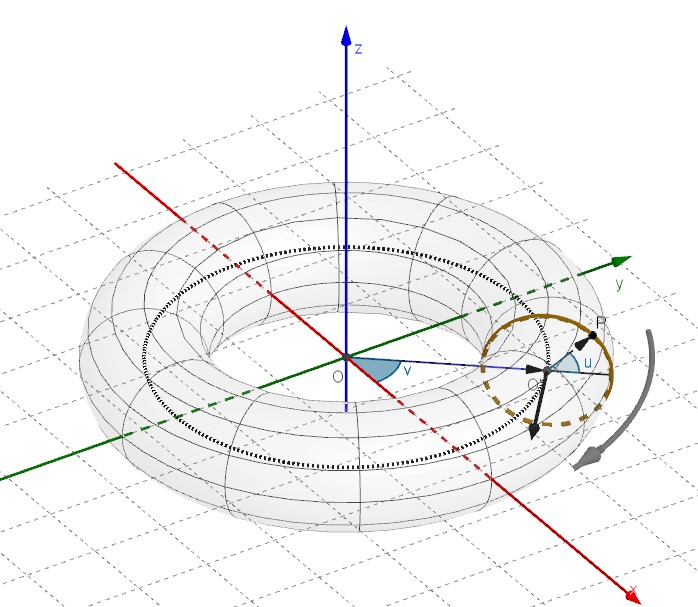
Un toro con centro nell’origine, avente l’asse ![]() come asse di rotazione e avente R e r come raggio maggiore e minore è descritto dalle equazioni parametriche
come asse di rotazione e avente R e r come raggio maggiore e minore è descritto dalle equazioni parametriche
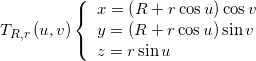
dove, se P è un punto sulla sua superficie, il parametro u è la posizione angolare di P sulla circonferenza la cui rotazione genera il toro e v è la posizione angolare del piano in cui si trova la circonferenza “ruotante” rispetto all’asse z.
La figura seguente mostra il significato delle equazioni parametriche sopra riportate.
L’equazione cartesiana del toro è:
![]()
oppure, eliminando la radice per ottenere una equazione polinomiale in x, y, z,
![]()
Analogie e differenze tra la superficie conica a il toro (e le loro equazioni)
Analogie
Entrambe le superfici sono elementi geometrici bidimensionali immersi in uno spazio tridimensionale. Pertanto, come avviene per ogni altra superficie, le loro equazoni parametriche, quando è possibile esprimerle con equazioni algebriche esplicite, sono definite tramite due parametri variabili che permettono di identificare le coordinate di ogni punto della superficie.
Entrambe le superfici sono superfici di rotazione, generate dalla rotazione di una semplice figura piana attorno a un asse.
Entrambe le superfici hanno un elevato grado di simmetria. Infatti esse sono simmetriche rispetto all’origine, rispetto agli assi cartesiani, e rispetto ai tre piani cartesiani. Sono anche simmetriche rispetto a tutti quei piani perpendicolari al piano orizzontale e passanti per l’origine.
Questo elevato grado di simmetria è anche deducibile dalla forma algebrica delle rispettive equazioni cartesiane, in cui le variabili x, y e z compaiono solamente con esponenti di grado pari cosicchè se si modifica il segno di una coordinata, ad esempio da x a –x, l’equazione non cambia.
Differenze
La superficie conica ha estensione illimitata ed è caratterizzata da un singolo parametro che determina la sua forma (l’angolo ![]() ).
).
Il toro ha invece una estensione finita ed è caratterizzato da due parametri che ne determinano la forma e la dimensione (il raggio maggiore R e il raggio minore r). In realtà la forma di un toro (indipendentemente da un fattore di scala) è determinata dal solo rapporto R/r.
Differenze topologiche (brevissimi cenni per i lettori più intrepidi)
Topologicamente il toro è il prodotto di due circonferenze e può essere espresso come
![]()
La definizione topologica di una superficie conica è un poco più complicata.
Il cono CX di uno spazio topologico X è lo spazio quoziente
![]()
del prodotto di X con l’intervallo unitario I = [0, 1].
Intuitivamente si può pensare a X come a un cilindro in cui una delle sue basi viene collassata (identificata o incollata) in un punto.
Più informalmente si può pensare a un toro come la figura che si ottiene a partire da un cilindro che viene deformato in modo da poter incollare la sua base superiore con quella inferiore. La superficie conica può invece essere vista come un cilindro deformato (strizzato) in una delle sue sezioni circolari in modo da farla coincidere con un punto.
Analogie e differenze nelle equazioni
Le equazioni parametriche di entrambe le superfici contengono le classiche funzioni goniometriche utili a rappresentare le rotazioni. Nella equazione della superficie conica, però, uno dei due parametri (s) agisce linearmente.
In entrambe le equazioni cartesiane le coordinate compaiono con esponenti di grado pari. La forma polinomiale dell’equazione della superficie conica è di secondo grado mentre quella del toro è di quarto grado.
Costruzione dell’equazione di una sezione torica
Prima di affrontare il problema di determinare l’equazione della curva di intersezione tra un toro e un piano è necessario esaminare come un piano possa essere rappresentato tramite una equazione e quale forma (cartesiana o parametrica) sia più utile per raggiungere lo scopo.
Il piano
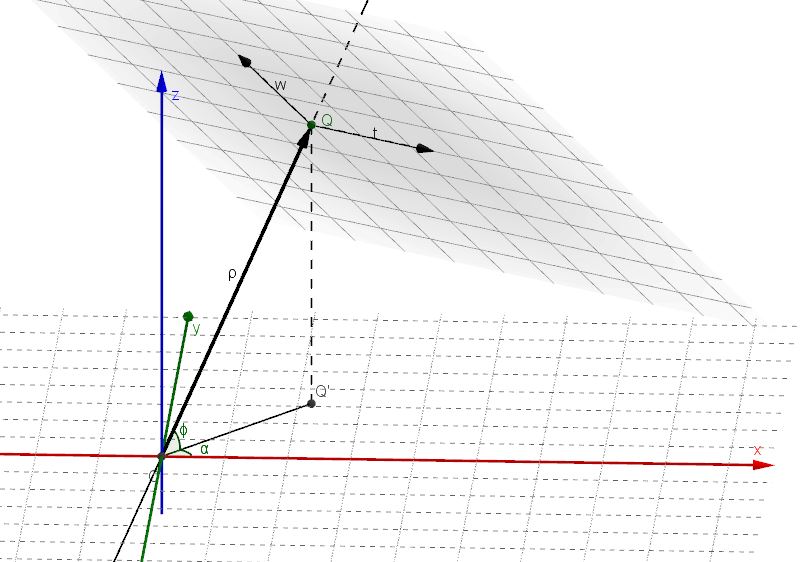
La posizione di un piano nello spazio può essere determinata tramite un vettore (con coda nell’origine) ad esso perpendicolare.
A sua volta questo vettore può essere identificato tramite i parametri ![]() ,
, ![]() e
e ![]() , dove:
, dove:
![]() è l’angolo che rappresenta la direzione della proiezione del vettore nel piano orizzontale
è l’angolo che rappresenta la direzione della proiezione del vettore nel piano orizzontale ![]() (angolo azimutale) rispetto all’asse x,
(angolo azimutale) rispetto all’asse x,
![]() è l’angolo che identifica l’elevazione del vettore rispetto al piano orizzontale xy.
è l’angolo che identifica l’elevazione del vettore rispetto al piano orizzontale xy.
![]() è il modulo (lunghezza) del vettore.
è il modulo (lunghezza) del vettore.
I componenti del vettore sono quindi ![]() .
.
Queste sono anche le coordinate del punto ![]() , proiezione ortogonale dell’origine
, proiezione ortogonale dell’origine ![]() sul piano.
sul piano.
L’equazione cartesiana del piano si può quindi scrivere come:
![]() .
.
In alternativa, le sue equazioni parametriche sono:
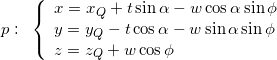
Nelle equazioni parametriche sopra riportate i parametri ![]() e
e ![]() possono essere interpretati come le coordinate di due assi cartesiani ortogonali giacenti nel piano intersecante, con origine nel punto
possono essere interpretati come le coordinate di due assi cartesiani ortogonali giacenti nel piano intersecante, con origine nel punto ![]() , dove
, dove ![]() è l’asse orizzontale (parallelo al piano
è l’asse orizzontale (parallelo al piano ![]() ) e
) e ![]() è l’asse verticale appartenente a questo piano e perpendicolare a
è l’asse verticale appartenente a questo piano e perpendicolare a ![]() . Questo nuovo sistema di riferimento bidimensionale tw, collocato nel piano intersecante il toro, svolgerà un ruolo importante nel seguito, essendo il sistema di riferimento ideale in cui riferire l’equazione della curva della sezione torica, dato che questa si troverà interamente (per definizione) in questo piano.
. Questo nuovo sistema di riferimento bidimensionale tw, collocato nel piano intersecante il toro, svolgerà un ruolo importante nel seguito, essendo il sistema di riferimento ideale in cui riferire l’equazione della curva della sezione torica, dato che questa si troverà interamente (per definizione) in questo piano.
La curva di intersezione tra il piano e il toro
Possiamo ora utilizzare le seguenti equazioni del toro e del piano per ottenere la curva di intersezione
![]()
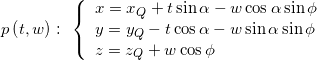 dove
dove 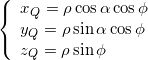
La strategia che si intende adottare è quella di inserire le equazioni parametriche in x, y, z del piano nell’equazione implicita del toro.
In questo modo otterremo una equazione implicita nelle nuove variabili t e w e dato che, come precedentemente osservato, queste variabili non sono altro che coordinate cartesiane ortogonali (dello stesso tipo delle usuali coordinate “xy”) all’interno del piano intersecante, l’equazione implicita che otterremo non sarà altro che l’equazione implicita della sezione torica, nel sistema di riferimento locale del piano intersecante.
Cominciamo
![]()
Sviluppando i quadrati l’espressione dentro la radice si semplifica in
![]()
quindi l’equazione diventa
![]()
Sviluppando ancora i quadrati si arriva a
![]()
se ora rinominiamo le variabili (t, w), che sono coordinate ortogonali nel piano secante, con le consuete lettere (x, y), l’equazione diventa
![]()
o anche, in forma polinomiale
![]()
da cui
![]()
Si tratta di una equazione nella forma
![]()
Si può notare che questa equazione rappresenta una curva simmetrica rispetto all’asse y ma non rispetto all’asse x.
L’equazione della sezione torica nello spazio
Dopo aver trovato l’equazione implicita che rappresenta la sezione torica in un sistema di riferimento bidimensionale che si trova nel piano intersecante, l’ultimo problema da affrontare è quello di dedurre, da questa equazione, quella in grado di rappresentare la curva nel sistema tridimensionale originale Oxyz.
Geogebra può tracciare il grafico di curve tridimensionali anche complesse nella vista grafica 3D se queste sono espresse in forma parametrica, con un singolo parametro, con un sistema di equazioni del tipo:
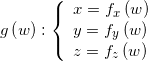
L’equazione in forma implicita precedentemente ricavata contiene però due parametri: t e w. In compenso sappiamo che la curva si trova interamente nel piano secante, di cui conosciamo l’equazione in forma parametrica. Quindi quello che si può fare è ricavare la relazione tra t e w dall’equazione in forma implicita, esprimendo un primo parametro in funzione del secondo, e usare poi l’equazione del piano che diventerà così una equazione parametrica con il solo secondo parametro.
L’esame dell’equazione implicita
![]()
suggerisce di esprimere t in funzione di w: ![]()
Con alcuni passaggi algebrici (non riportati) si arriva all’espressione:
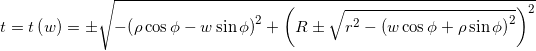
Non proprio semplice o particolarmente significativa, sembra.
Comunque, inserendo l’espressione appena ricavata nell’equazione del piano, otterremo l’equazione in forma parametrica della nostra sezione torica nello spazio:
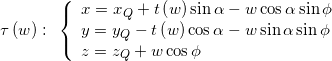
e potremo visualizzare questa curva tramite Geogebra.
Una sorpresa! (il ritorno del cono)
L’equazione implicita della sezione torica nel piano intersecante il toro
![]()
può essere riscritta utilizzando le consuete variabili (x, y) al posto di (t, w)
![]()
Se cerchiamo di semplificare un poco questa espressione, magari eliminando la radice con un opportuno cambio di variabili, potremmo avere l’idea di porre
![]()
cioè, al posto di ![]() useremo l’espressione
useremo l’espressione
![]()
In pratica applichiamo la mappa
![]()
Con questa trasformazione l’equazione della sezione torica diventa;
![]()
ovvero, nel sistema di riferimento ![]()
![]()
![]()
![]()
![]()
![]()
Con apparente e insperata fortuna siamo riusciti a fare diverse semplificazioni. Bene!
Alla fine abbiamo ottenuto l’equazione di una coppia di ellissi, ma possiamo fare ancora meglio e trasformarle in una coppia di circonferenze se poniamo ![]() . Quindi
. Quindi
![]()
Questa equazione rappresenta una coppia di circonferenze nel piano yz.
I due centri hanno coordinate ![]() e il raggio comune è
e il raggio comune è ![]() .
.
Quindi, con un opportuno cambio di variabili, la nostra sezione torica viene trasformata in una coppia di circonferenze.
Ma la stessa cosa può valere anche in senso opposto: una coppia di circonferenze possono “generare“, con una opportuna trasformazione, una sezione torica. Sembra interessante.
Più precisamente, se partiamo da due circonferenze collocate nel piano yz
![]()
e applichiamo la trasformazione ![]() definita da
definita da
![]()
otteniamo una sezione torica!
A questo punto è naturale chiedersi quale sia il significato geometrico della trasformazione ![]() che muta magicamente due circonferenze (e qui torna in mente la definizione topologica del toro) in una sezione torica.
che muta magicamente due circonferenze (e qui torna in mente la definizione topologica del toro) in una sezione torica.
La variabile y non è stata modificata, ma la nuova variabile z è una funzione delle vecchie variabili (x, y) espressa dall’equazione
![]()
e questa è, nello spazio tridimensionale, l’equazione di una superficie conica!
In questo caso la superficie conica non è circolare dato che le sezioni che si ottengono tagliandola con piani orizzontali ![]() sono ellissi i cui semiassi hanno misura
sono ellissi i cui semiassi hanno misura ![]() e
e ![]() .
.
Il vertice del cono, inoltre, ha coordinate ![]() .
.
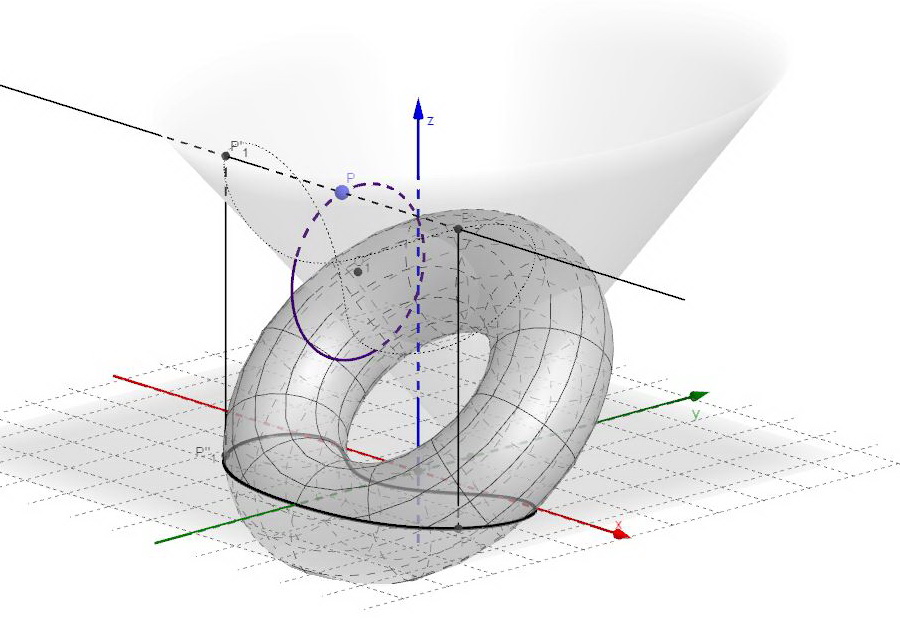
Quindi, per chiarire e schematizzare i precedenti passaggi, possiamo definire la seguente procedura, curiosa e inattesa, per generare una sezione torica:
- Si sceglie una delle due circonferenze precedentemente ricavate, giacenti nel piano yz e si prende un punto appartenente alla stessa:
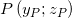
- Si determina l’intersezione della retta passante per P perpendicolare al piano yz e la superficie conica
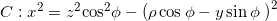
In generale, quando la retta effettivamente interseca il cono, ci saranno due punti di intersezione: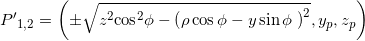
- Si proiettano questi due punti sul piano xy. Le coordinate di questa nuova coppia di punti saranno:
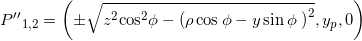 .
.
Questi due punti appartengono a una sezione torica giacente nel piano xy. - Muovendo il punto P lungo la circonferenza prescelta i punti P’ tracceranno una curva sulla superficie del cono e la proiezione di questa curva sul piano xy è la sezione torica corrispondente all’insieme di parametri utilizzati
 .
.
La seguente figura mostra la procedura di costruzione seguita:
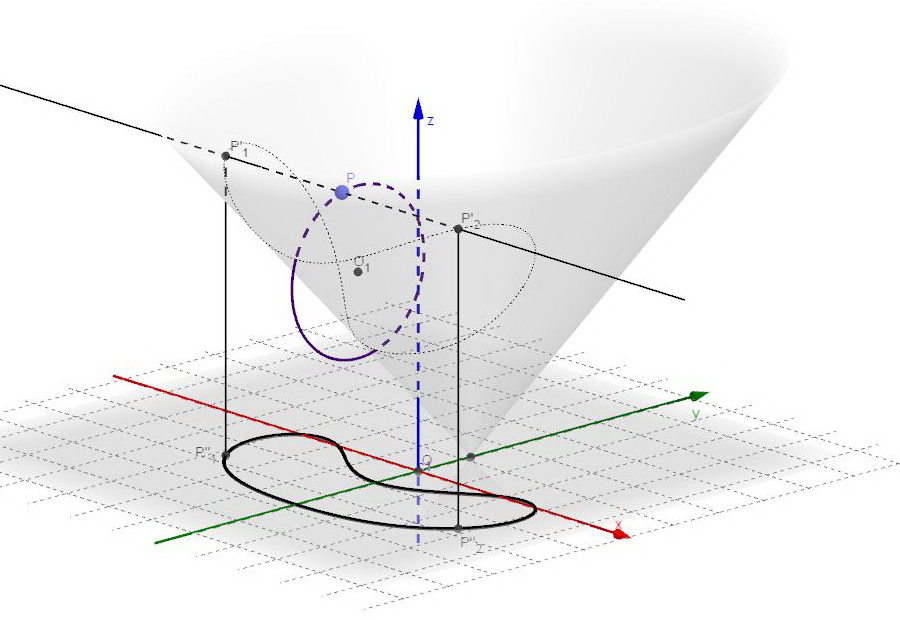
fig. 12 – Costruzione, a partire dai punti di una circonferenza e tramite una superficie conica, della sezione torica
In effetti con la procedura specificata sopra non abbiamo fatto altro che costruire la curva di intersezione tra un cilindro con un cono e ottenere la sezione torica come proiezione sul piano xy di questa curva.
Con questo metodo la sezione torica viene tracciata sul piano xy, che svolge quindi il ruolo di piano intersecante. Ma dato che questo piano intersecante deve tagliare il toro formando un certo angolo (![]() ) con il piano equatoriale del toro, per ripristinare la configurazione relativa originale tra piano e toro dobbiamo ora pensare a un toro inclinato, con il suo piano equatoriale che forma lo stesso angolo
) con il piano equatoriale del toro, per ripristinare la configurazione relativa originale tra piano e toro dobbiamo ora pensare a un toro inclinato, con il suo piano equatoriale che forma lo stesso angolo ![]() con il piano xy.
con il piano xy.
Nella seguente figura abbiamo rappresentato, oltre al cono, anche il toro inclinato che viene intersecato dal piano xy e abbiamo verificato che la curva precedentemente ottenuta è effettivamente la sezione torica corrispondente.
In conclusione, nell’indagare le proprietà delle sezioni toriche siamo partiti da un confronto tra toro e cono e tra sezioni toriche e sezioni coniche, abbiamo poi derivato l’equazione della sezione torica (equazione di quarto grado) e, con qualche passaggio algebrico, abbiamo “scoperto” che la stessa curva può essere ricavata anche come proiezione su un piano della curva di intersezione tra un cono e un cilindro (dove entrambe queste due superfici hanno equazioni di secondo grado). Pertanto possiamo dire che la superficie conica risulta collegata al toro più strettamente del previsto, in quanto costituisce una specie di ponte nella relazione astratta e qualitativa
![]()
Le sezioni coniche con Geogebra
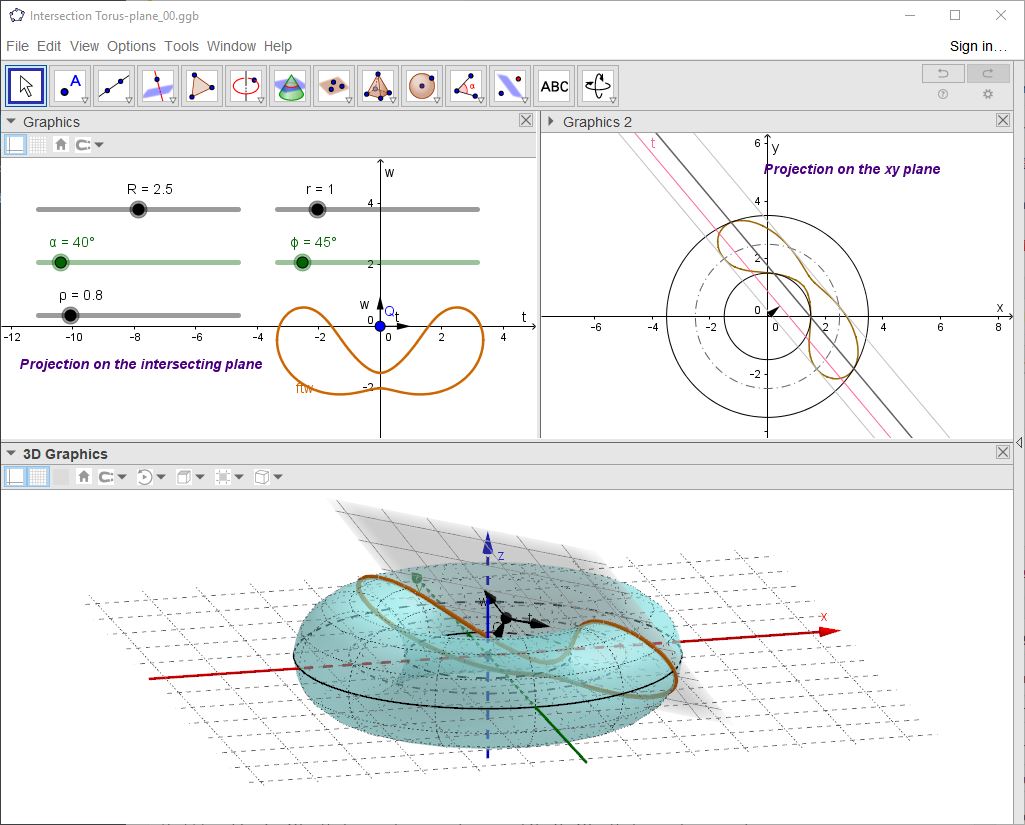
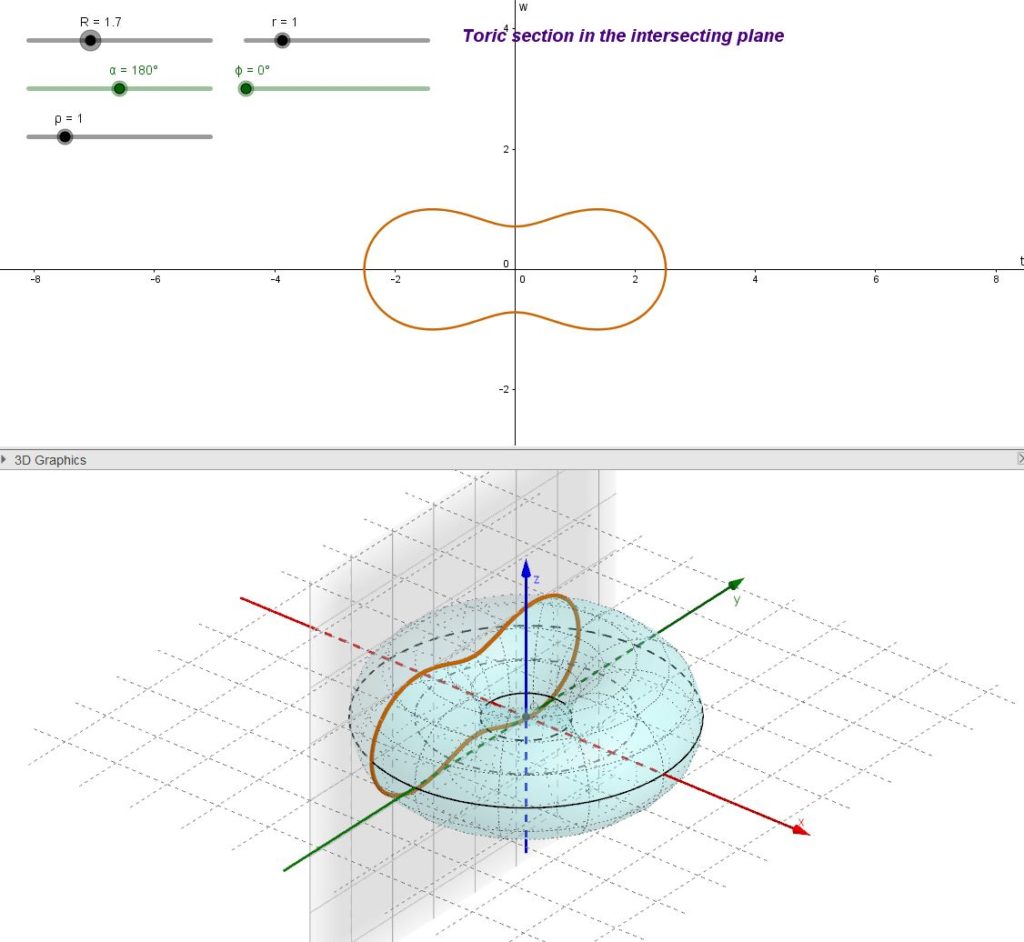
Nella pagina https://www.lucamoroni.it/simulations/intersection-torus-plane-simulation/ è presentata una simulazione interattiva in cui è possibile generare e visualizzare diverse sezioni toriche variando i diversi parametri geometrici.
Il file di Geogebra può anche essere visualizzato nel portale dei materiali di Geogebra (https://ggbm.at/MmTVuXYk) o, meglio, scaricato come file con estensione “.ggb” (https://www.geogebra.org/material/download/format/file/id/Vp95FtPQ o Intersection Torus-plane) ed eseguito localmente sul PC tramite il programma gratuito Geogebra Classico disponibile in questa pagina.
Referimenti (in inglese)
https://en.wikipedia.org/wiki/Torus
https://en.wikipedia.org/wiki/Toric_section
https://en.wikipedia.org/wiki/Conical_surface
https://en.wikipedia.org/wiki/Cone_(topology)
Sym, Antoni (2009), “Darboux’s greatest love”, J. Phys. A: Math. Theor. 42 (2009) 404001
Geogebra material: Torus-plane intersection
Rational families of circles and bicircular quartics – OPUS 4 – ThomasWernerDissertation.pdf
Brieskorn-Knörrer (1986), Plane Algebraic Curves, Birkhäuser
Ultima modifica: 4 maggio 2020