[note: a slightly improved version of this article has been published by arXiv with the title “The toric sections: a simple introduction” and can be downloaded as pdf at https://arxiv.org/pdf/1708.00803 or from this website (The toric sections: a simple introduction)]
Overview
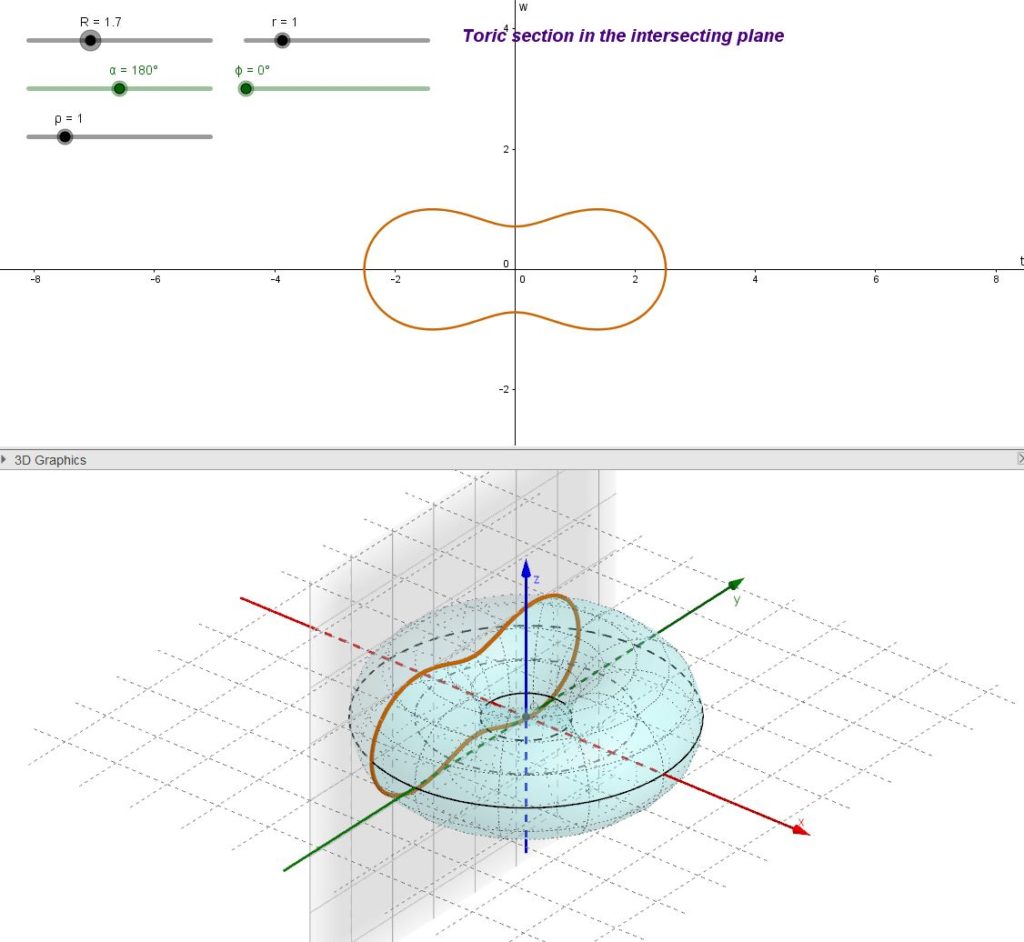
The curve of intersection of a torus with a plane is called toric section. Even if both surfaces are rather simple to define and are described by rather simple equations, the toric section has a rather complicated equation and can assume rather interesting shapes.
In this article I’ll discuss some properties of this curve, investigate its differences with the most renowned conic section, show how to build its general quartic equation, explore how a toric section can also be generated by intersecting a cylinder with a cone and finally describe how it is possible to represent it in the 3D Graphics view of Geogebra.
In the article only elementary algebra is used, and the requirements to follow it are
some notion of goniometry and of tridimensional analytic geometry.
The torus and the toric sections
The torus surface is generated by rotating a circle with radius r around an axis coplanar with the same circle, following a second circle of radius R. The two radii r and R are so the parameters that identify the torus’ shape. In the following lines (if not otherwise specified) we’ll always assume that ![]() (to avoid self-intersections), and that, in Cartesian coordinates, the equatorial plane is the xy plane and the axis of rotation is the z axis.
(to avoid self-intersections), and that, in Cartesian coordinates, the equatorial plane is the xy plane and the axis of rotation is the z axis.
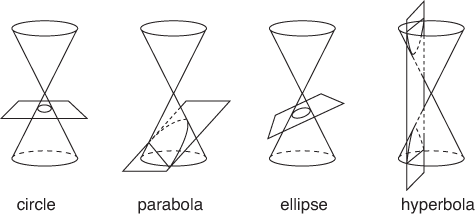
A toric section is the analogue of a conic section as it is the intersection curve of a torus with a plane just as a conic section is the intersection curve between a conical surface and a plane.
But whilst conic sections have a (deserved) renown also due to their multiple connections with many fundamental problems of (classical) physics, toric sections are often relegated to the realm of mathematical curiosities and exotic curves. Yet…
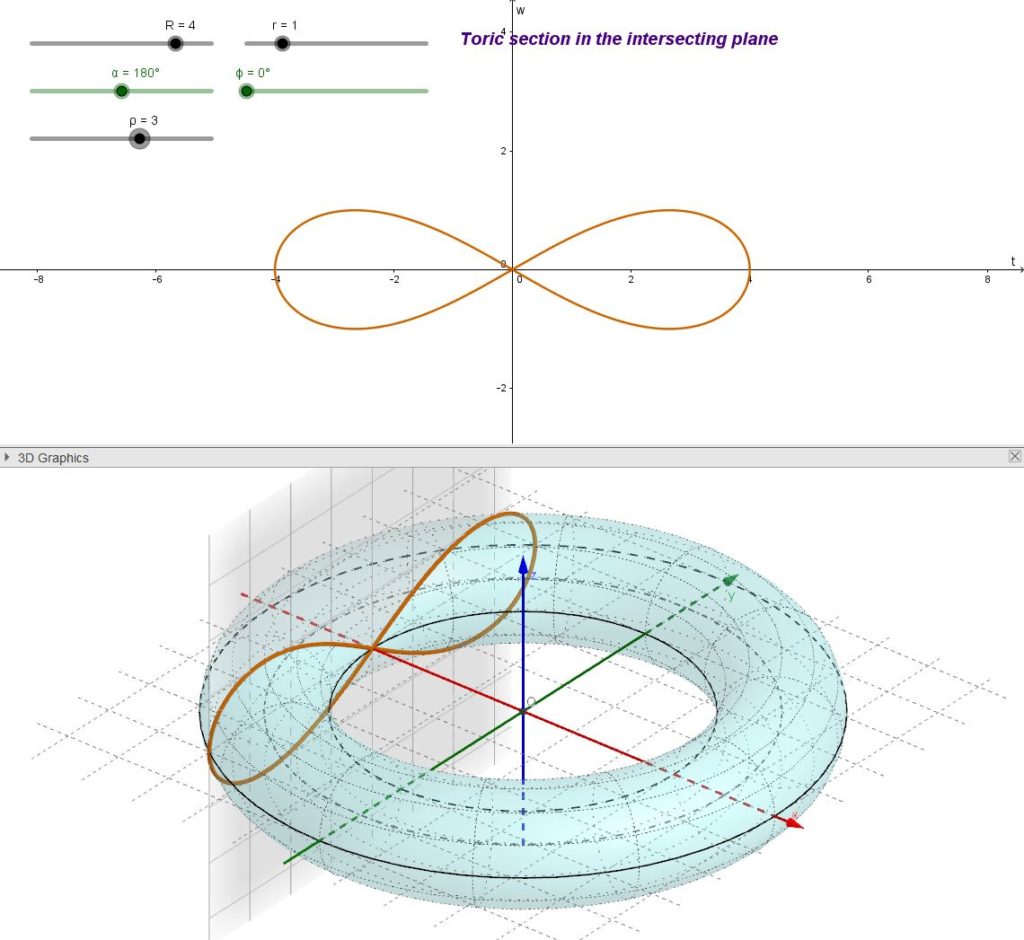
The variety of the toric sections is quite rich and the study of the case when sectioning planes are parallel to the symmetry axis of the torus dates back to antiquity. The corresponding curves are usually called “the spiric sections of Perseus” after their discoverer (circa 150 BC). Among them, one can distinguish Cassini’s curves (in particular, Bernoulli’s lemniscate).
[from: Sym, Antoni (2009), “Darboux’s greatest love”, J. Phys. A: Math. Theor. 42 (2009) 404001]
The variety of toric sections
In this section we’ll shortly describe and present some particular toric sections that also have an historical relevance. Amongst them Villarceau’s circles, Cassini’s ovals, Bernoulli’s lemniscates and the Hippopedes of Proclus.
The central toric sections and the Villarceau’s circles
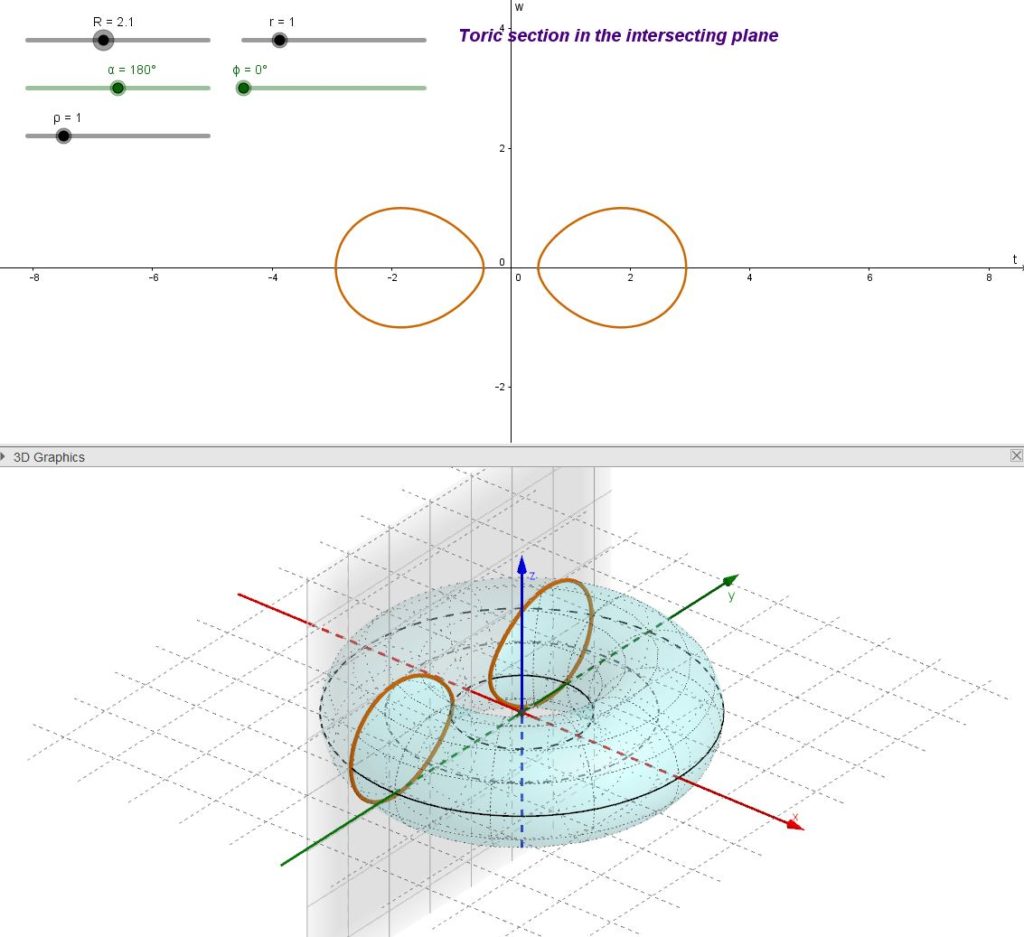
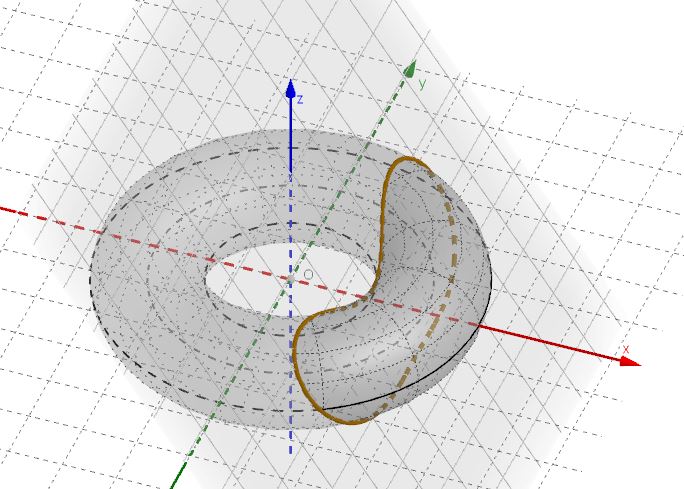
A toric section in which the cutting plane passes through the center of the torus is called central toric section.
Central toric sections can be circles in the following cases:
- the intersecting plane is the equatorial plane
- the intersecting plane is perpendicular to the equatorial plane
- the intersecting plane touches the torus in two isolated points.
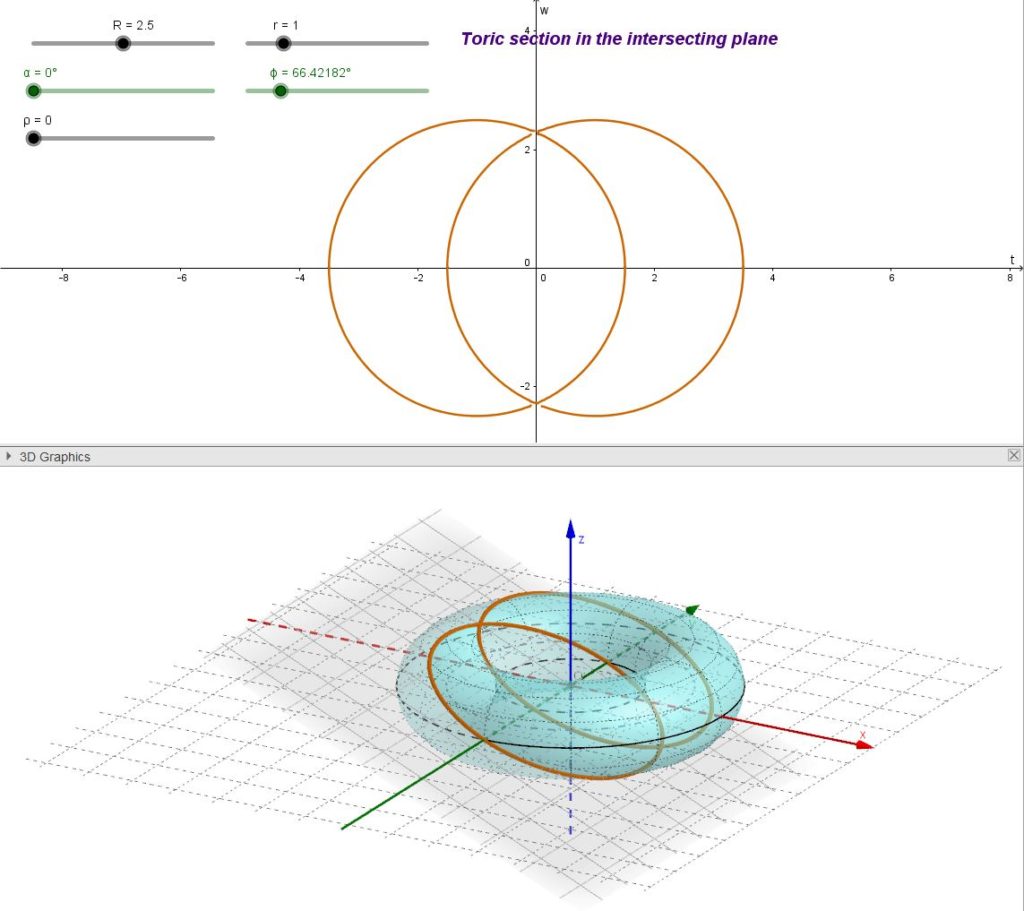
The last (less banal) case produces two circles that are called Villarceau’s circles.
Central toric sections – other sections
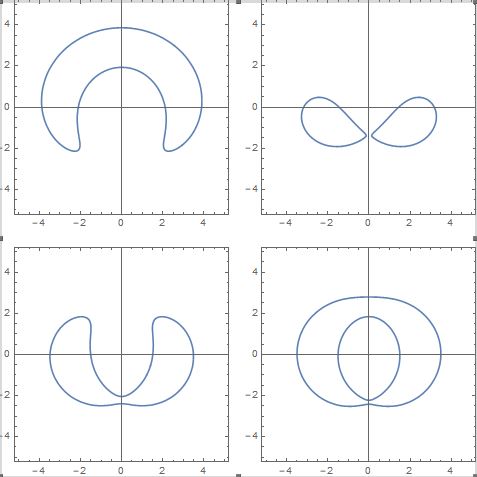
It must be noted that, if some central conic section generates circles, not all central toric sections are circles as in the following examples.
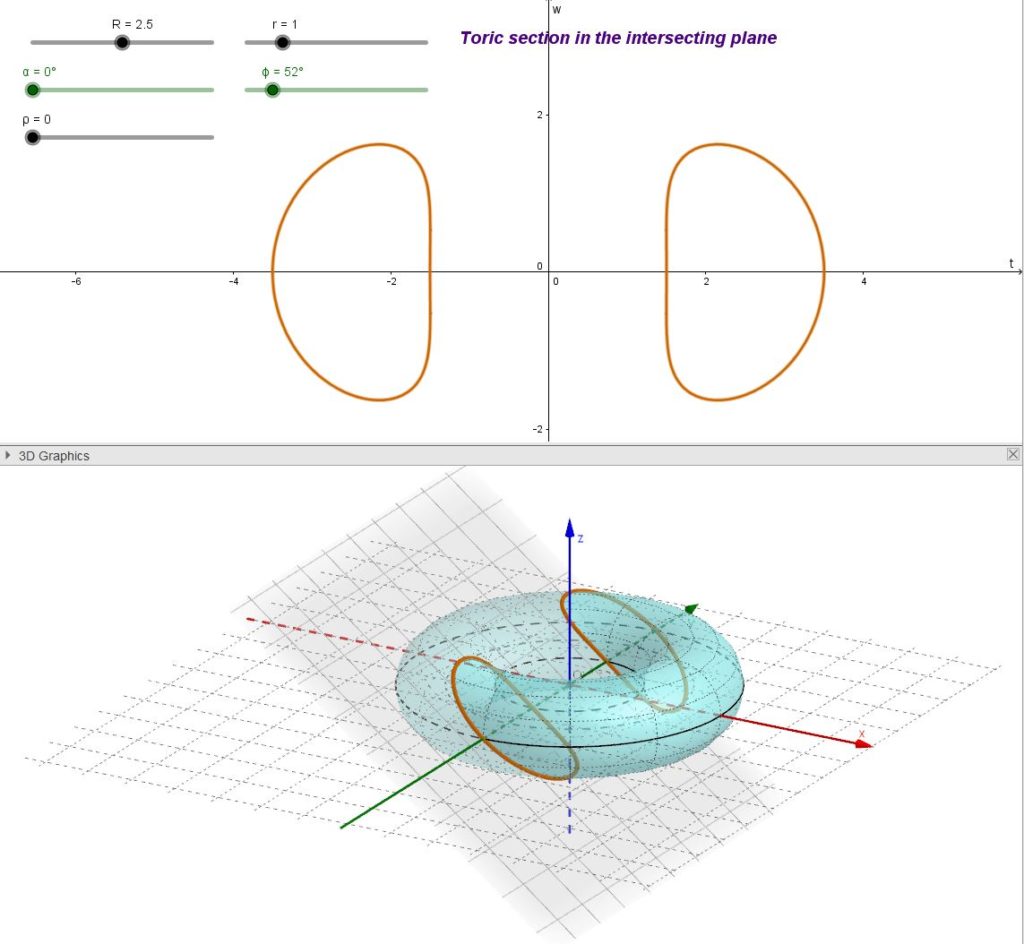 |
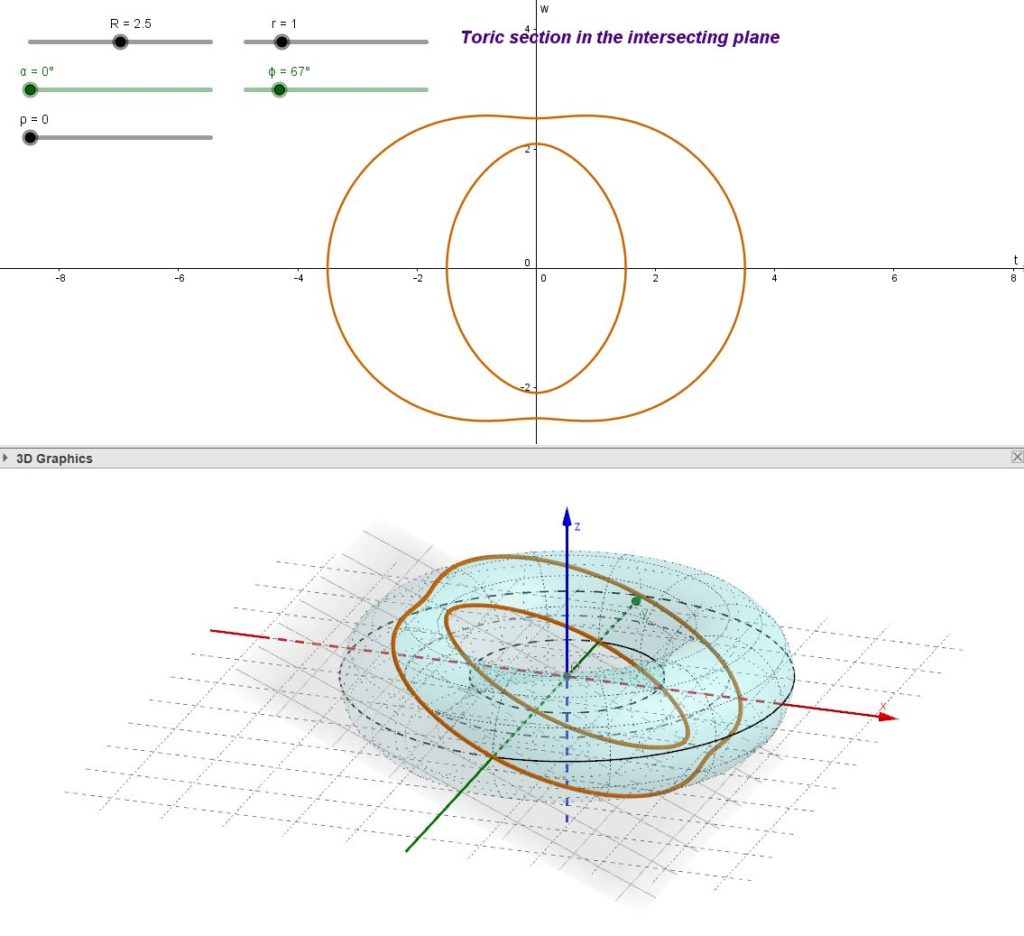 |
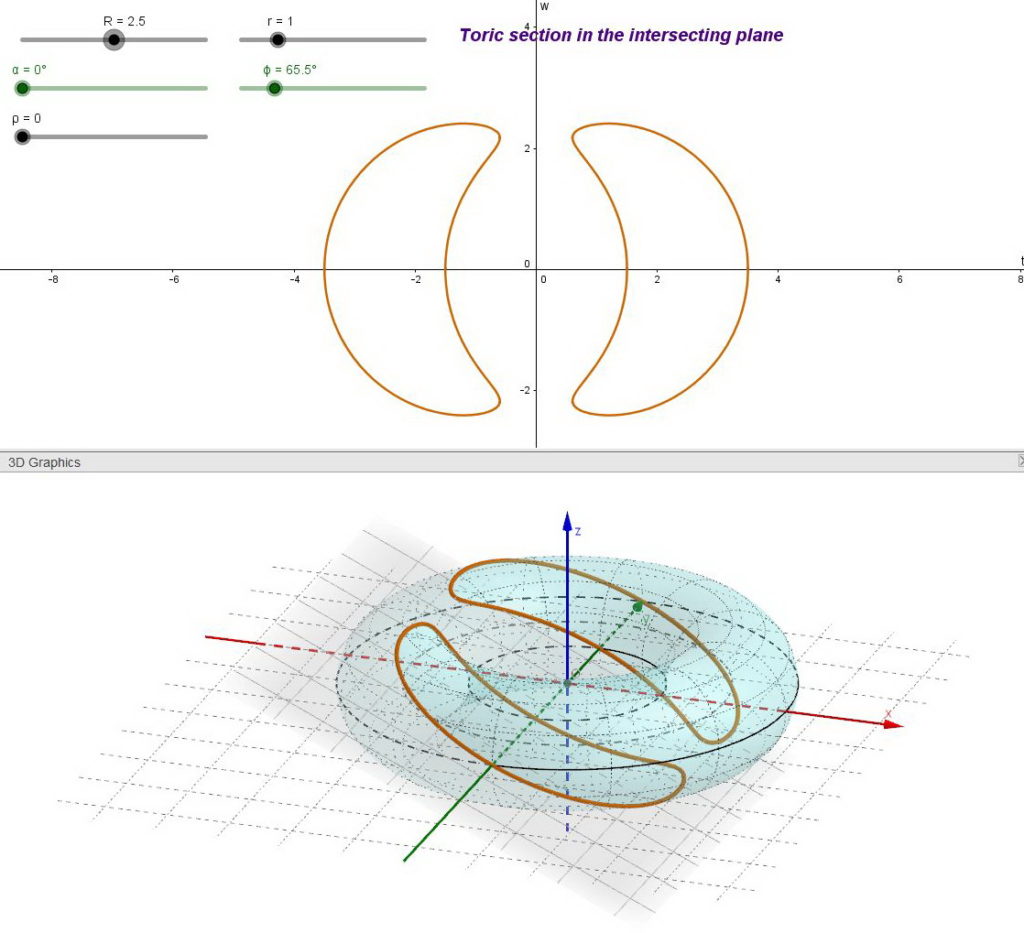 |
| fig. 04 – Generic central toric sections | ||
Spiric sections
The toric section generated by an intersecting plane that is parallel to the torus axis (or perpendicular to the torus equatorial plane) is called a spiric section. The name comes from the ancient Greek word “σπειρα” for torus.
Fall in this category Cassini’s ovals and Bernoulli’s Lemniscates.
Cassini’s ovals are spiric sections in which the distance of the cutting plane to the torus axis equals the radius r of the generating circle.
An interesting alternative definition of a Cassini’s oval is that of the set of points P such that the product of their distances to two fixed points F1 and F2 is constant:
![]()
This definition recalls that of the ellipse but here we must use the product of the distances instead of the sum.
If the focal distance is ![]() , the Cassini’s ovals parameters, with reference to the torus intersected, have the values
, the Cassini’s ovals parameters, with reference to the torus intersected, have the values ![]() and
and ![]() .
.
 |
 |
| fig. 05 – Two different Cassini’s ovals | |
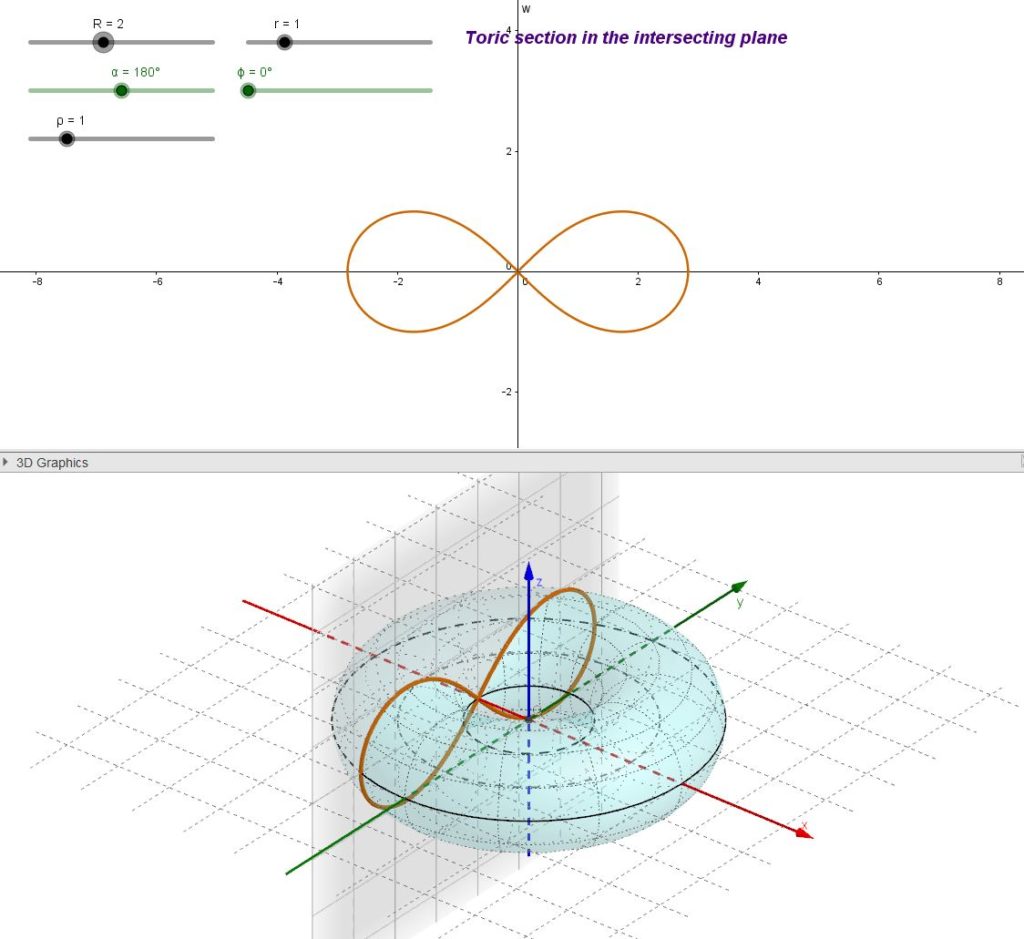
Bernoulli’s lemniscate is, in turn, a special case of a Cassini’s oval. It is generated as a Cassini’s oval with the further requirement that ![]() . In practice the intersecting plane must be tangent to the inner equator of the torus.
. In practice the intersecting plane must be tangent to the inner equator of the torus.
The lemniscate of Bernoulli can also be defined as the set of points P such that the product of their distances to two fixed points F1 and F2 is constant and is also equal to the semi focal distance squared:
![]() where
where ![]() .
.
As a curiosity we can note that this lemniscate curve, representing an “eight” lying down, has been used as the symbol for mathematical “infinity” (∞) starting from the 17th century.
If we drop the requirement ![]() that characterizes Cassini’s ovals but keep the condition that the intersecting plane is tangent to the interior circle (so that it must be
that characterizes Cassini’s ovals but keep the condition that the intersecting plane is tangent to the interior circle (so that it must be ![]() ) we have the family of curves called Hippopedes of Proclus.
) we have the family of curves called Hippopedes of Proclus.
Generic toric sections
There are many other toric sections that are neither central sections nor spiric sections. This means that the cutting plane is generically slanted with respect to the torus equatorial plane and that it has a non-zero distance from the center of the torus. Here are some examples:
Toric sections and conic sections
The torus surface is generated by rotating a generating circle around an axis coplanar with the circle itself. In other words it is produced by moving around a first circle of center O the center O’ of a second circle, providing that the second circle plane stays perpendicular to the tangent line to the first circle in O’.
On the other hand a conical surface (right circular conical surface) can be generated by rotating a straight line around another straight line, providing that the first intersect the second, keeping fixed the angle between the two lines.
The main difference between the two surfaces can then summarized as “circle rotated around a line” vs. “line rotated around line“.
Since in a Cartesian coordinate system a circle is described by a second order equation and a line by a first order equation and that the rotation involves following a circular path, it can be anticipated that, in a Cartesian coordinate system, the equation of a toric section can be a quartic whilst, for a conic section, a quadratic equation suffices.
The conical surface equation and the torus equation
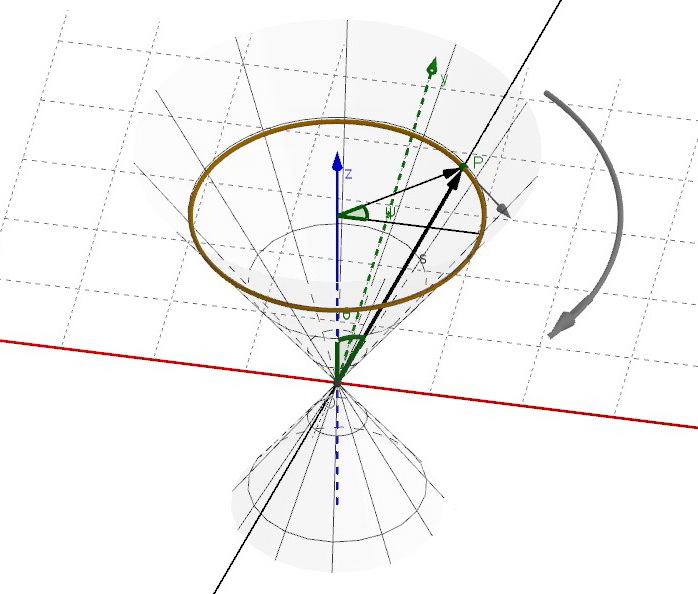
A right circular conical surface of aperture ![]() , whose axis is the
, whose axis is the ![]() coordinate axis, and whose apex is the origin O, is described by the parametric equations
coordinate axis, and whose apex is the origin O, is described by the parametric equations
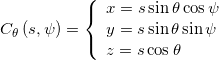
where, if P is a point on the surface, the parameter s is the coordinate of P along the oriented line OP and the parameter ![]() is the angle of rotation of P around the z axis.
is the angle of rotation of P around the z axis.
The following figure explains the meaning of the parametric equations.
In Cartesian coordinates the conical surface has implicit equation
![]()
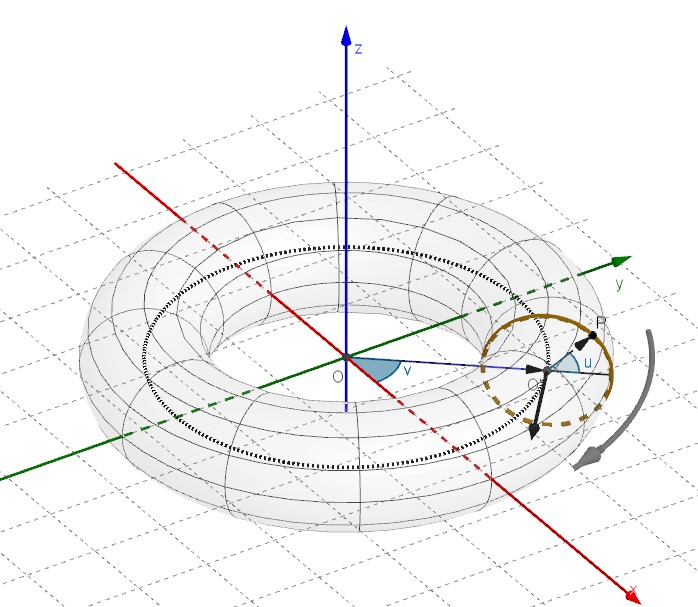
A torus centered in the origin with the ![]() axis as axis of revolution and with R and r as the major and minor radii, is described by the parametric equations
axis as axis of revolution and with R and r as the major and minor radii, is described by the parametric equations
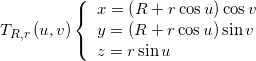
where, if P is a point on the surface, the parameter u is the angular position of P on the revolving circle and v is the angular position of the plane of the revolving circle with respect to the z axis.
The following figure explains the meaning of above parametric equations.
the torus Cartesian (implicit) equation is:
![]()
or (eliminating the square root to obtain a polynomial equation in x, y, z)
![]()
Analogies and differences between the conical surface and the torus (and their equations)
Analogies
Both surfaces are bi-dimensional geometric objects immersed in a three dimensional space and so, like for any other surface, their parametric equations (if they can be made explicit), are always controlled by two variable parameters that set the coordinates of every point of the surface.
Both surfaces can be generated as surface of revolution, rotating a simpler figure around an axis.
Both surfaces have a very high degree of symmetry, as they are symmetric not only with respect to the origin, but also with respect of each of the three Cartesian coordinate axes (and this implies that they are also symmetric with respect to the three Cartesian planes). They are also symmetric with respect to all planes that are perpendicular to the horizontal plane and are running through the origin.
This high level of symmetry follows form the simple fact that the Cartesian equations of both surfaces only contains the squares of the three Cartesian coordinates, so that changing, say, x with (-x) has no effect on the equations.
Differences
The conical surface is unbounded and is characterized by one single parameter determining its shape (the angle ![]() ).
).
The torus has a finite extension and is characterized by two parameters determining its shape (the major radius R and the minor radius r) and size, but, actually its “scale free” shape is governed by the R/r ratio).
Topological differences (quick note for the more intrepid readers)
Topologically a torus is the product space (or Cartesian product) of two circles, that can be expressed as
![]()
The topological definition of a conical surface is a little more complicated.
The cone CX of a topological space X is the quotient space:
![]()
of the product of X with the unit interval I = [0, 1].
Intuitively we make X into a cylinder and collapse (identify or glue) one end of the cylinder to a point.
More informally a torus can be thought of as a cylindrical surface with the top and bottom circles glued together, whilst a conical surface can be seen as a cylindrical surface in which one of its circular section is collapsed to a point.
Analogies and differences in the equations
In the parametric equations of both surfaces there are trigonometric functions (to represent the rotations), but in the conical surface equation one of the parameters (s) acts linearly.
The Cartesian equations are given in implicit form and the Cartesian coordinates always appears with an even grade order. The polynomial form of the conical surface is of second order, while the polynomial form of the torus is fourth order.
Building the equation of a toric section
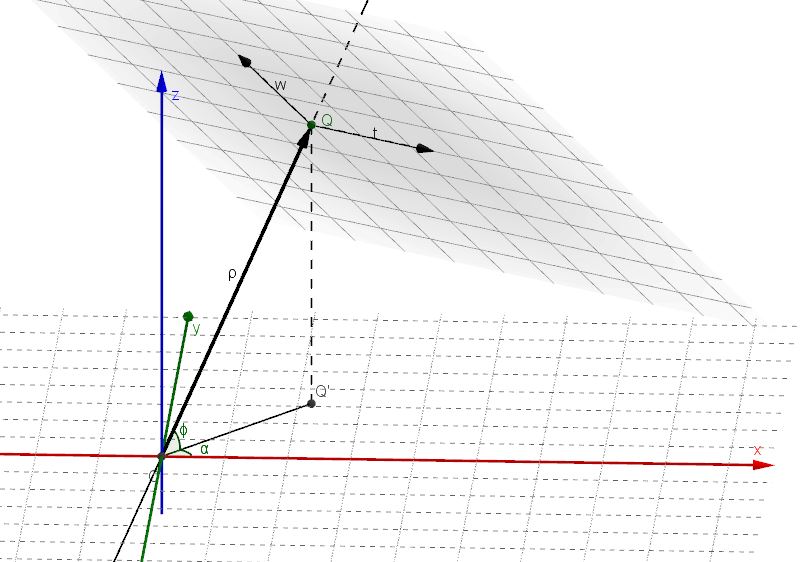
Before attacking the problem to find the equation of the curve of intersection between a torus and a plane it’s necessary to examine how a plane can be described by an equation and which form (Cartesian or parametric) is more convenient for the purpose.
The plane
The plane can be identified by the vector orthogonal to it. So let’s use the parameters ![]() ,
, ![]() and
and ![]() that set the position of the normal vector
that set the position of the normal vector ![]() through the origin.
through the origin.
![]() is the direction in the horizontal
is the direction in the horizontal ![]() plane (azimuthal angle),
plane (azimuthal angle), ![]() is the direction with respect of the horizontal plane (elevation angle) and
is the direction with respect of the horizontal plane (elevation angle) and ![]() is the modulus (length) of the vector.
is the modulus (length) of the vector.
The components of the vector are then ![]() . These are also the coordinates of the point
. These are also the coordinates of the point ![]() , projection of the origin
, projection of the origin ![]() on the plane.
on the plane.
The Cartesian equation of the plane is then:
![]() .
.
and its alternative parametric equations are:
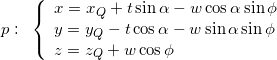
With above parametric equations the parameters ![]() and
and ![]() can be interpreted as the embedded orthogonal Cartesian axes in the plane starting from the point
can be interpreted as the embedded orthogonal Cartesian axes in the plane starting from the point ![]() (plane origin), where
(plane origin), where ![]() is the horizontal axis (parallel to the
is the horizontal axis (parallel to the ![]() plane) and
plane) and ![]() is the vertical axis in this plane (perpendicular to
is the vertical axis in this plane (perpendicular to ![]() ).
).
The intersection curve between the plane and the torus
We can now use the following equations of the torus and the plane to get the intersection curve
![]()
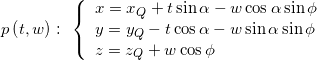 where
where 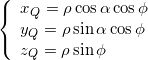
We’ll plug in the x, y, z parametric equations of the plane in the torus implicit equation. In so doing we’ll then get an implicit equation in the new variables t and w and since these variables are just the “xy” coordinates inside the intersecting plane, this implicit equation will be nothing but the implicit equation of the toric section as seen in the intersecting plane.
Let’s start
![]()
Expanding the squares, the expression inside the square root simplifies to
![]()
so our equation will be
![]()
Expanding the squares we finally get
![]()
that is, renaming the (t, w) orthogonal coordinates in the plane with the usual letters (x, y) the equation will be
![]()
or, in polynomial form,
![]()
that can be written as
![]()
Above equation is in the form
![]()
It can be noted that this equation is symmetric with respect to the x axis (but not with respect to the y axis).
The equation of the toric section in space
Having found an implicit equation giving the toric section represented in the intersecting plane, the last problem is to translate this equation in space and get an equation presenting the same curve in tridimensional space.
Geogebra can draw even complicated curves in the 3D graphics view if they are expressed in a parametric form, with a single parameter, of the type:
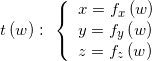
Anyway, the implicit equation previously found contains two parameters, t and w. Furthermore we know that the curve lies on the intersecting plane.
What can be done is find the relation between t and w given by the implicit equation, expressing one parameter as a function of the other, and use the plane equation with the second parameter.
The examination of the implicit equation
![]()
suggests to express t as a function of w ![]()
With some algebra we get to
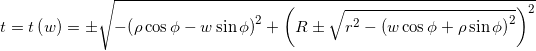
Not much meaningful and simple, I admit…
Our curve in space will then be
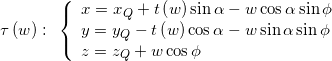
A surprise! (the conical bridge)
The implicit equation of the toric section in the intersecting plane
![]()
can be written as follows by renaming the variables (t, w) with the usual symbols (x, y)
![]()
If we try to simplify it a little with some change of variables and get rid of the square root, we could have the idea to make the transformation
![]()
that is, we set ![]() as
as
![]()
So we apply the geometric transformation that maps ![]() to
to ![]()
With this mapping the toric section equation becomes
![]()
that is (in the ![]() space)
space)
![]()
![]()
![]()
![]()
![]()
We have obtained the equation of an ellipse. But we can do even better and make it a circle by setting ![]() , so it is
, so it is
![]()
This is the equation of a pair of circles in the yz plane.
The centers are ![]() ,
, ![]() and the common radius is
and the common radius is ![]() .
.
The meaning of all this is that if we start with the following two circles in a yz plane
![]()
and apply the transformation ![]() defined by
defined by
![]()
we get a toric section!
Now what is the geometric meaning of ![]() ?
?
The y variable is unchanged, but the z variable is related to the variables (x, y) by the equation
![]()
Above is, in tridimensional space, the Cartesian equation of a conical surface with vertex ![]() .
.
This is not a circular conical surface and the sections of this surface with the horizontal planes ![]() are ellipses with semi axes of length
are ellipses with semi axes of length ![]() and
and ![]() .
.
So, to summarize the previous passages, here’s a curious unexpected way to trace a toric section.
- Start form one of the two circles in the yz plane (one is enough) and choose a point on it:
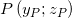
- Find the intersection between the line through P perpendicular to the plane yz and the conical surface
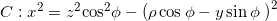
In general, if the line actually intersect the cone, there will be two intersection points: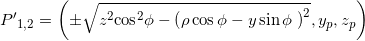
- Project this two points on the xy plane. They will be:
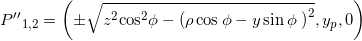 . These two points are points of the toric section.
. These two points are points of the toric section. - By moving the point P on the circle, the points P’ will trace a curve on the conical surface and the projection of this curve on the xy plane is the toric section corresponding to the set of parameters
 used.
used.
The following figure shows the construction method
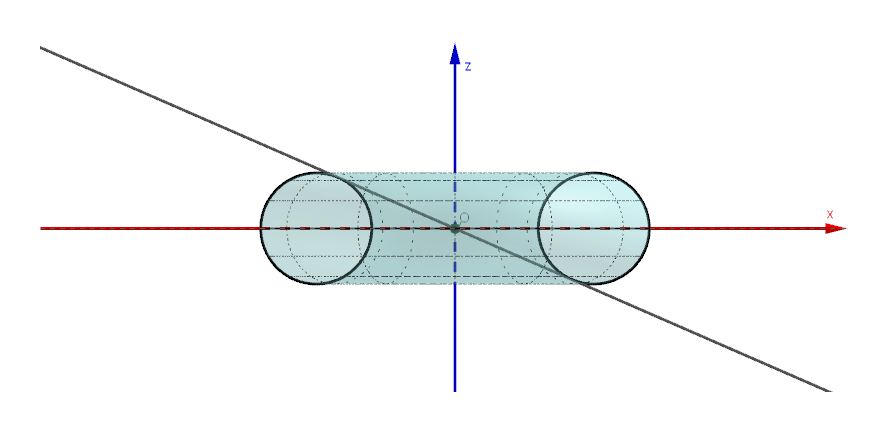
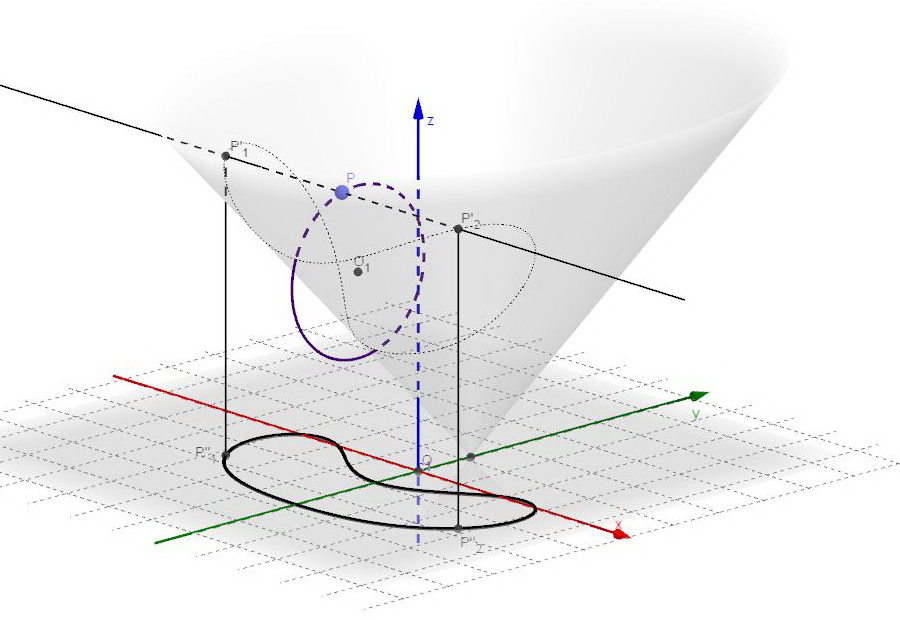
Actually we have done nothing but intersecting the conical surface with a cylinder and have verified that the projection of the curve of intersection on the xy plane is a toric section,
With this method we trace the toric section on the intersecting plane that, in this case, is the xy plane.
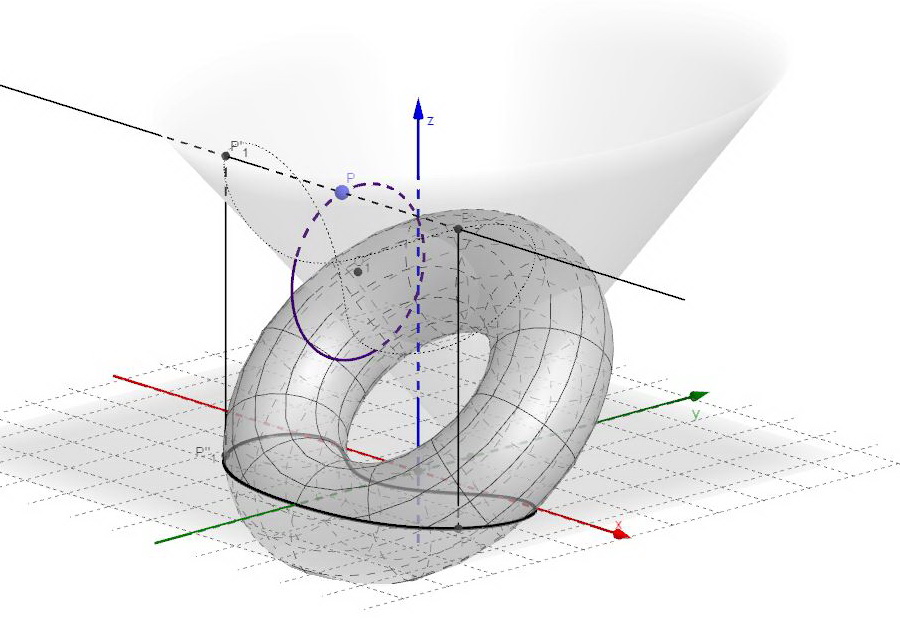
So the torus intersected must have to be tilted by the angle ![]() to reproduce the initial figure (torus intersection with an oblique plane) with respect to the xy plane.
to reproduce the initial figure (torus intersection with an oblique plane) with respect to the xy plane.
Here’s the tilted torus intersecting the xy plane. The previously obtained curve is actually a toric section.
In conclusion, we have started with a comparison of toric and conic sections, derived the toric section equation (fourth grade), and, with some algebraic manipulation, found that the same toric section equation can also be seen has the projection on a plane of a cone-cylinder intersection (where both surfaces have second grade equations). The conical surface, then, is more closely related to the torus than expected as it enters, as a sort of bridge (fig.14), in the approximate abstract equivalence relation
![]()
The toric section in Geogebra
In the page https://www.lucamoroni.it/simulations/intersection-torus-plane-simulation/ there is an interactive simulation about generating toric sections together with some explanation of the interactive commands.
The Geogebra file can also be seen in Geogebra’s material repository (https://ggbm.at/MmTVuXYk) or, better, downloaded as a “.ggb” file (https://www.geogebra.org/material/download/format/file/id/Vp95FtPQ or Intersection Torus-plane) and run locally on the PC. The free Geogebra Classic desktop program is available at this page.
References
https://en.wikipedia.org/wiki/Torus
https://en.wikipedia.org/wiki/Toric_section
https://en.wikipedia.org/wiki/Conical_surface
https://en.wikipedia.org/wiki/Cone_(topology)
Sym, Antoni (2009), “Darboux’s greatest love”, J. Phys. A: Math. Theor. 42 (2009) 404001
Geogebra material: Torus-plane intersection
Rational families of circles and bicircular quartics – OPUS 4 – ThomasWernerDissertation.pdf
Brieskorn-Knörrer (1986), Plane Algebraic Curves, Birkhäuser
Last edited: 04 May 2020

Can you please assist. I need to find the surface area of a torus-cylinder intersection.
https://math.stackexchange.com/questions/1675074/torus-cylinder-intersection
Hi Dayton
I’ve answered your question (or I hope so) in https://math.stackexchange.com/questions/1675074/torus-cylinder-intersection
Mr. Moroni,
Thank you for your thorough treatment of this subject, and the beautiful illustrations which help to visualize all of the surfaces at each step.
I was wondering if you could offer some advice on developing an implicit equation of a elliptic torus – the surface formed when a circle is moved through an elliptical path.
I was able to work this out using parametric equations, but it is much more difficult to see a clear solution to the implicitization.
Thank you.
Hi William
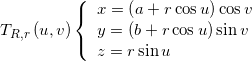
The parametric equations for you “elliptic torus” with semi-axis a and b should be
The parameter v can easily be eliminated by squaring the first and second equation and summing them.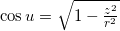 .
.
To eliminate the parameter u you could try to substitute
Afterwards you should rearrange the terms and make some squaring to eliminate the roots.
It seems a very nasty calculation. I gave up.
Ok. This is what I got:
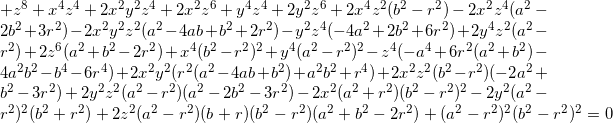
I saw your (10 Oct. 2021) twitter post! This topic is related to my web page about hippopedes of Proclus:
https://users.pfw.edu/CoffmanA/pov/spiric.html
The page has a link to my 2007 paper about these curves, and pictures of a cone-paraboloid intersection which projects to a hippopede.
I found your model on Geogebra.
I’m wondering if there is a way to get the length of the circumference and/or the area of the intersection as represented by the “Projection on the intersecting plane”.
Maybe this can already be found in your model but i didn’t figure it out actually.
Some assistance would be great.
thx
I’m sorry. Too much time has passed since my research and I don’t remember almost anything about it. I suggest you to ask your question to some helpful site, like https://math.stackexchange.com making reference to my published paper on arXiv: https://arxiv.org/abs/1708.00803
No worries 🙂
Unfortunately actually nobody replied to my post (https://math.stackexchange.com/questions/4632240/length-of-circumference-and-or-area-by-intersection-of-torus-and-plane). But i found myself a solution for the specific case, where the intersection produces two separate areas (https://mathcurve.com/courbes2d/spiric/spiric.shtml). That allowed me to set up a ridle (https://coord.info/GCA3WE4)
thx for the reply 🙂
I appreciate