Intersection of a torus with a plane (simulation)

[note: the full article is available at https://www.lucamoroni.it/toric-sections/ and has been published by arXiv with the title “The toric sections: a simple introduction”. arXiv paper can be downloaded as pdf at https://arxiv.org/pdf/1708.00803 or from this website (The toric sections: a simple introduction)]

This Geogebra applet is about exploring the intersection curve of a torus with a plane.

The file can be seen in Geogebra’s material repository (https://ggbm.at/MmTVuXYk) or, better, downloaded as a “.ggb” file (https://www.geogebra.org/material/download/format/file/id/Vp95FtPQ) and run locally on the PC. The free Geogebra Classic desktop program is  available at this page.

The plane

The plane can be positioned using the parameters \alpha, \phi and \rho that set the position of the normal vector \vec u through the origin.

\alpha is the direction in the horizontal xy plane (azimuthal angle), \phi is the direction with respect of the horizontal plane (elevation angle) and \rho is the modulus (length) of the vector.

The components of the vector are then \vec u = \left( {\rho \cos \alpha \cos \phi ,\rho \sin \alpha \cos \phi ,\rho \sin \phi } \right).These are also the coordinates of the point Q, projection of the origin O on the plane.

The Cartesian equation of the plane is then:
p:\,\,\,\left( {x - {x_Q}} \right)\cos \alpha \cos \phi + \left( {y - {y_Q}} \right)\sin \alpha \cos \phi + \left( {z - {z_Q}} \right)\rho \sin \phi = 0.

and its alternative parametric equations are:

p:\,\,\,\left\{ {\begin{array}{*{20}{l}} {x = {x_Q} + t\sin \alpha - w\cos \alpha \sin \phi }\\ {y = {y_Q} - t\cos \alpha - w\sin \alpha \sin \phi }\\ {z = {z_Q} + w\cos \phi } \end{array}} \right.

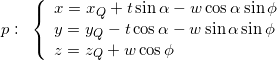
With above parametric equations the parameters t and w can be interpreted as the embedded orthogonal Cartesian axes in the plane starting from the point Q (plane origin), where t is the horizontal axis (parallel to the xy plane) and w is the vertical axis in this plane (perpendicular to t).

The torus

The torus position is fixed, with center in the origin and the z axis as  axis of symmetry (or axis of revolution). Anyhow its parameters R (major radius) and r (minor radius) can be changed through the respective sliders.The parametric equation of the torus surface is:

\left\{ {\begin{array}{*{20}{l}} {x = \left( {R + r\cos v} \right)\cos u}\\ {y = \left( {R + r\cos v} \right)\sin u}\\ {z = r\sin u} \end{array}} \right.

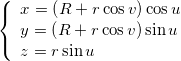
Alternatively, the torus Cartesian equation is:

{\left( {\sqrt {{x^2} + {y^2}} - R} \right)^2} + {z^2} = {r^2}

The views

In the 3D graphics (bottom frame) there is the spatial representation of the plane, the torus and the intersection curve. Click and drag the mouse to change the point of view.

In the Graphics view (upper left frame,  the one with the sliders) is represented the intersection curve as seen in the intersecting plane. Note that it won’t change with changes of the angle \alpa as this parameter just rotates the plane around the torus symmetry axis.

In the Graphics 2 view (upper right frame) there is a representation of the 3D view projected in the xy plane. The slanted lines showed here are a visual aid to help imagine how the p plane develops in the invisible z dimension. They are:

  • intersection of the p plane with the plane z=0;
  • intersection of the 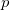p plane with the planes 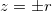z = \pm r (the horizontal planes tangent to the torus above and below);
  • intersection of the 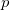p plane with the plane 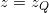z = {z_Q} that is, the projection of the 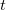t axis on the 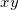xy plane.

References

https://en.wikipedia.org/wiki/Torus
https://en.wikipedia.org/wiki/Toric_section

 

Last edited: 24 july 2017

7 thoughts on “Intersection of a torus with a plane (simulation)”

  1. J Knudsen

    Hi, great work. I came across your article when researching toric sections for a youtube video I’m currently working on. Wanted to ask for your permission to use your applet for making animations of various toric sections. You will of course be credited in the video description, and I will link to your website if you wish.

    Reply ↓
  2. Alex Fraser

    Hello. Wonderful work. I am not sure how to contact you directly by email.
    Would I be able to ask for your permission to use your Geogebra applet to create a couple of toric sections for a figure in an academic paper I am writing? I would give you credit in the paper and include a link to your website and toric sections paper in arXiv. Thank you!

    Reply ↓
  3. Tamas Fabian

    Dear Mr. Luca Moroni,
    I write you,  to ask you about torus intersection.
    1. I read your report about torus-plane intersection:  The toric sections: a simple introduction 
     It is a great idea, the possibility to substitute the torus-plane intersection with cone-cylinder intersection.
    And you write all very clearly. I think, I solved the torus-plane intersection with Mthematica 12.

    2. Then I read your other report in Stack Exchange about turus-cylinder intersection;
    https://math.stackexchange.com/questions/1675074/torus-cylinder-intersection  
    All clear. I drew the intersection curve with GeoGeabra and Mathematica too.

    That’s  my problem, it is a special case.The axe of cylinder perpendicular to axe of torus.
    So we get a relative simply solution. But this position is a rare and lucky case in the practic.

    My question. What happens, if I have a cylinder with arbitrary axis in translated position?
    I try to compute the equation of intersection curve, but I can’t. Would you help me?
    Where can I find an example? I think this question is solved, and I looking for solution.
    How can I compute and draw the equation of intersection curve if I have a torus and cylinder with equation:
    (x^2 + y^2 + z^2 + 100 – 16 )^2 – 4*100 (  x^2 + y^2) == 0 

    xcyl = t/Sqrt[2] + 2 Sqrt[2] Sin[fi] + 5;
    ycyl = 4* Cos[fi] – 12;
    zcyl = t/Sqrt[2] – 2 Sqrt[2] Sin[fi];

    Sincerely,
    Tamas Fabian

    Reply ↓
    1. Luca M Post author

      Hello. I’m afraid that the problem you are proposing is solvable (in theory) but computationally too difficult. I (and Mathematica) gave up. Sorry.

      Reply ↓
  4. Lajos László

    Dear Luca Moroni, I made a MATLAB program constructing ITERATIVELY the ellipse inscribed into a given pentagon.
    In view of your paper “Ellipse inscribed in a pentagon”, however, it seems that this is of little relevance, or??
    Thanks for any comments, L. László.

    Reply ↓

Leave a Reply

Your email address will not be published. Required fields are marked *