Questo applet di Geogebra applet serve a esplorare la curva di intersezione tra un toro e un piano.
Il file può essere visualizzato nel portale dei materiali di Geogebra (https://ggbm.at/MmTVuXYk) o, meglio, scaricato come file “.ggb” (https://www.geogebra.org/material/download/format/file/id/Vp95FtPQ) ed eseguito localmente su PC. Il programma Geogebra Classico per desktop è scaricabile in questa pagina.
Il piano
Il piano può essere posizionato nello spazio tramite i parametri ![]() ,
, ![]() e
e ![]() che definiscono la direzione e il modulo del vettore
che definiscono la direzione e il modulo del vettore ![]() che parte dall’origine e arriva perpendicolarmente al piano.
che parte dall’origine e arriva perpendicolarmente al piano.
![]() è la direzione lungo il piano orizzontale
è la direzione lungo il piano orizzontale ![]() (angolo azimutale),
(angolo azimutale), ![]() è la direzione rispetto al piano orizzontale (angolo di elevazione) e
è la direzione rispetto al piano orizzontale (angolo di elevazione) e ![]() è il modulo (lunghezza) del vettore, o anche la distanza del piano dall’origine.
è il modulo (lunghezza) del vettore, o anche la distanza del piano dall’origine.
Le componenti del vettore sono quindi ![]() .Queste sono anche le coordinate del punto
.Queste sono anche le coordinate del punto ![]() , proiezione dell’origine
, proiezione dell’origine ![]() sul piano.
sul piano.
L’equazione cartesiana del piano è allora:
![]() .
.
oppure, in alternativa, le sue equazioni in forma parametrica sono:
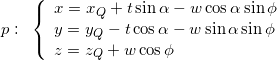
Con le equazioni parametriche sopra riportate i parametri ![]() e
e ![]() possono essere interpretati come gli le coordinate dei punti del piano lungo una coppia di assi cartesiani ortogonali collocati nel piano stesso e aventi origine nel punto
possono essere interpretati come gli le coordinate dei punti del piano lungo una coppia di assi cartesiani ortogonali collocati nel piano stesso e aventi origine nel punto ![]() , dove
, dove ![]() è l’asse orizzontale (parallelo al piano
è l’asse orizzontale (parallelo al piano ![]() e
e ![]() è l’asse a questo perpendicolare.
è l’asse a questo perpendicolare.
Il toro
La posizione del toro è fissa, con il suo centro di rotazione nell’origine e avente l’asse ![]() come asse di rivoluzione. Comunque è possibile modificare, tramite slider, i suoi parametri
come asse di rivoluzione. Comunque è possibile modificare, tramite slider, i suoi parametri ![]() (raggio maggiore) e
(raggio maggiore) e ![]() (raggio minore).
(raggio minore).
Le equazioni parametriche della superficie torica sono:
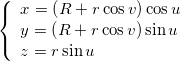
e la sua equazione cartesiana è:
![]()
Le viste
Nlla finestra Grafici 3D (riquadro inferiore) è riportata la rappresentazione spaziale del toro, del piano e della loro curva di intersezione. Cliccando e trascinando il mouse in un’area vuota di questa vista si può modificare il punto di visuale.
Nella finestra Grafici (riquadro superiore a sinistra, quello con gli slider) è rappresentata la curva di intersezione collocata nel piano intersecante. Si noti che questa curva non cambia con modifiche dell’angolo ![]() dato che questo parametro non fa altro che ruotare il piano attorno all’asse di simmetria del toro.
dato che questo parametro non fa altro che ruotare il piano attorno all’asse di simmetria del toro.
Nella finestra Grafici 2 (riquadro superiore a destra) è riportata una rappresentazione della vista 3D proiettata sul piano ![]() . Le linee inclinate che vi appaiono sono un aiuto visivo per riuscire a immaginare come il piano intersecante
. Le linee inclinate che vi appaiono sono un aiuto visivo per riuscire a immaginare come il piano intersecante ![]() si sviluppa nella dimensione
si sviluppa nella dimensione ![]() , invisibile in questa vista. Esse sono:
, invisibile in questa vista. Esse sono:
- intersezione del piano
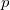 con il piano
con il piano 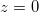 ;
; - intersezioni del piano
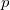 con i piani
con i piani 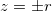 (i piani orizzontali tangenti al toro superiormente e inferiormente);
(i piani orizzontali tangenti al toro superiormente e inferiormente); - intersezione del piano
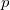 con il piano
con il piano 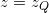 ovvero la proiezione dell’asse
ovvero la proiezione dell’asse 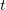 nel piano
nel piano 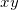 .
.
Referimenti
https://en.wikipedia.org/wiki/Torus
https://en.wikipedia.org/wiki/Toric_section
Ulltima modifica: 29 agosto 2017