I segreti dell’ellisse: dimostrazione geometrica dell’equivalenza delle sue due definizioni

Ogni volta che cerco di approfondire la teoria della gravitazione di Newton mi imbatto, prima o poi, nell’ellisse e nelle sue proprietà geometriche.
Dopo diversi anni sono sempre più convinto che raggiungere una migliore comprensione dell’ellisse e delle sue numerose proprietà geometriche, anche le più sottili e nascoste, sia un passaggio fondamentale per capire più a fondo le teorie fisiche e matematiche in cui essa compare.

La definizione geometrica dell’ellisse può essere formulata tramite due definizioni alternative ma equivalenti:

A) L’ellisse è il luogo dei punti ( $P$ ) del piano per i quali si mantiene costante la somma delle distanze di questi punti da due punti dati, chiamati fuochi ( $F_1$ e $F_2$ ). In linguaggio matematico vale quindi la relazione:

$\overline {PF_1} + \overline {PF_2} = \text{costante} = 2a$ (dove $a$ è il semiasse maggiore dell’ellisse).

B) L’ellisse è il luogo dei punti ( $P$ ) del piano per per cui si mantiene costante il rapporto tra la distanza di $P$ da un punto dato fissato (chiamato fuoco) $F_1$ e la distanza di $P$ da una retta data detta (chiamata direttrice) $d$ . In linguaggio matematico vale quindi la relazione:

$\overline{PF_1}/ \overline{PH}=\text{costante}=e$ (dove $e$ è l’eccentricità dell’ellisse ed $0<e<1$ ).

L’equivalenza delle due definizioni può essere dimostrata in modo molto semplice ed elegante utilizzando, in geometria solida, le sfere di Dandelin e sfruttando la definizione di ellisse come sezione conica.

D’altra parte, dato che l’ellisse è una curva piana mi sono spesso chiesto se fosse possibile dimostrare l’equivalenza di queste due definizioni usando la geometria piana, senza dover ricorrere a una terza dimensione.

Un altra possibile strada è quella della geometria analitica, che richiede di collocare gli elementi che definiscono l’ellisse (fuochi, direttrice) in un sistema di assi cartesiani.

Ho cercato a lungo una dimostrazione geometrica che utilizzasse la geometria piana e i metodi classici della geometria euclidea.

Ma, dato che non ho mai trovato una tale dimostrazione in rete o nei testi di riferimento , qualche anno fa, nel lontano 2008, ho cercato di costruirne una da me.

Quasi per caso ho riscoperto in questi giorni (ottobre 2016), quella dimostrazione di diversi anni fa e l’ho trovata interessante e potenzialmente ricca di spunti per possibili altre investigazioni geometriche, anche se necessitante di qualche affinamento.

Nel presente articolo è riportata la dimostrazione che ho individuato allora, essenzialmente immutata nei suoi aspetti essenziali, ma alla quale ho aggiunto qualche dettaglio in più.
In essa sono sfruttate diverse relazioni e proprietà tratte dalla pura geometria piana e qualche intuizione personale.

La prima parte I) riguarda la dimostrazione che la definizione A) implica la definizione B). La seconda parte II) (in parte solo abbozzata in quanto si basa in gran parte sui passaggi della prima parte, ripercorsi in ordine inverso) è volta a dimostrare che la definizione B) implica la definizione A).
Nella terza parte III), ho aggiunto una costruzione geometrica dell’ellisse (rispecchiante la definizione B) trovata in un testo classico (1895) sulle sezioni coniche.

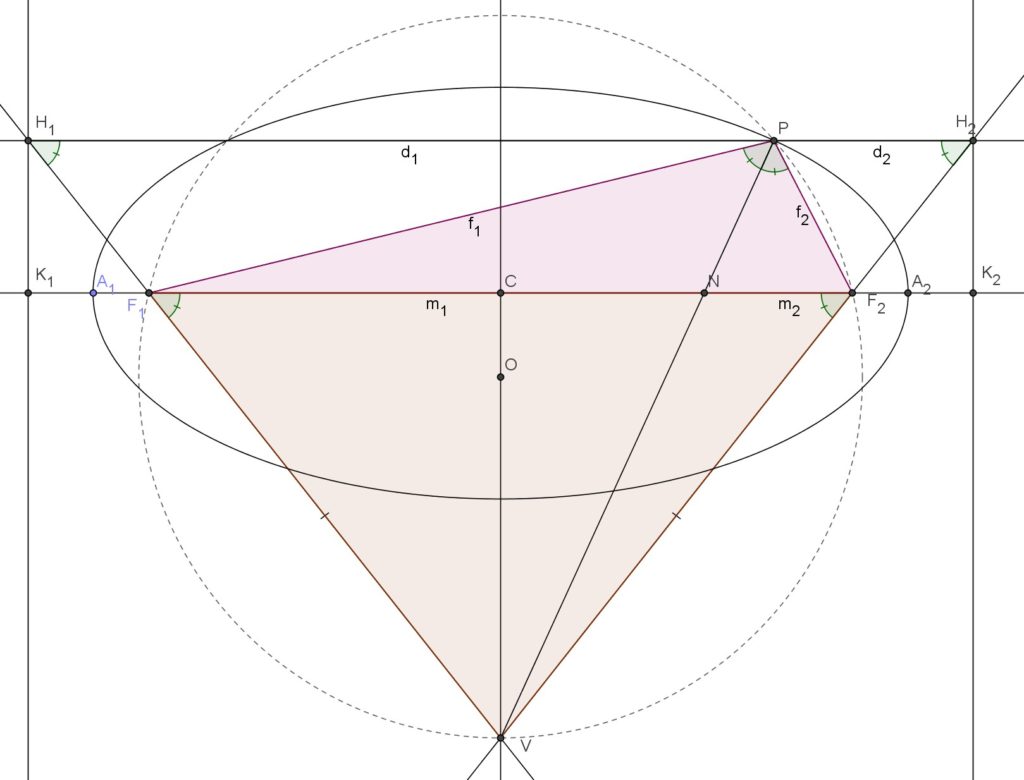
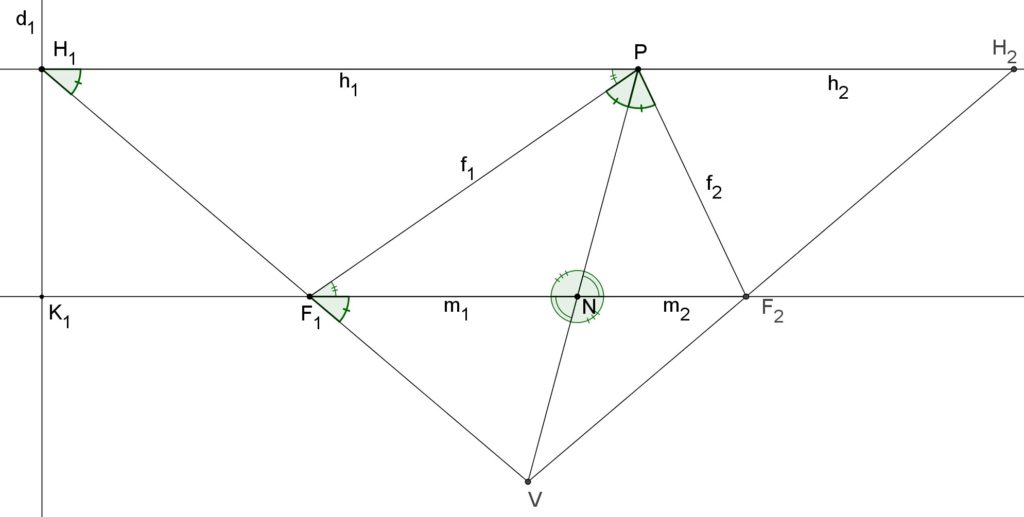
fig.1: equivalenza delle due definizioni dell’ellisse: definizione “fuoco-fuoco” e “fuoco-direttrice”

I) Prima parte: A) $\rightarrow$ B)

Data una ellisse definita come luogo dei punti per i quali è costante la somma delle distanze da due punti fissi $F_1$ e $F_2$ , allora, per ogni punto $P$ appartenente all’ellisse deve essere $\overline{PF_1}=e\cdot \overline{PH_1}$ , dove $\overline{PH_1}$ è la distanza di $P$ da una opportuna retta (chiamata direttrice) perpendicolare alla retta congiungente $F_1$ e $F_2$ .

Dimostrazione

Siano

$\overline{F_1F_2}=2c; \; \; \overline{PF_1}+\overline{PF_2}=2a; \; \; c/a=e; \; \; \overline{PF_1}=f_1; \; \; \overline{PF_2}=f_2$

Per prima cosa si consideri il triangolo $F_1F_2P$ e si costruisca la circonferenza circoscritta a tale triangolo.

L’asse del segmento $F_1F_2$ interseca la circonferenza (nell’arco $\stackrel {\frown} {F_1F_2}$ che non include $P$ ) nel punto $V$ (il quadrilatero $VF_1F_2P$ è quindi un quadrilatero ciclico).

Sia $N$ l’intersezione della retta $PV$ con la retta passante per $F_1$ e $F_2$ . Il punto $N$ suddivide il segmento $F_1F_2$ in due parti le cui lunghezze sono $\overline{NF_1}=m_1$ e $\overline{NF_2}=m_2$ .

Siano poi $H_1$ e $H_2$ i punti in cui la retta passante per $P$ parallela a $F_1F_2$ interseca le rette $VF_1$ e $VF_2$ e siano $\overline{PH_1}=d_1; \; \; \overline{PH_2}=d_2$

Dato che $\overline{F_1V}=\overline{F_2V}$ , per le proprietà delle corde di una circonferenza, segue che gli angoli $V\widehat{P}F_1$ e $V\widehat{P}F_2$ sono congruenti, e che $PV$ è la bisettrice dell’angolo $F_1\widehat{P}F_2$ . Possiamo anche dire che $F_1\widehat{P}N=N\widehat{P}F_2=F_1\widehat{F_2}V=\alpha$

Applicando il teorema della bisettrice al triangolo $F_1PF_2$ si ottiene la proporzione

$f_1:m_1=f_2:m_2$

Da questa proporzione si possono poi ricavare le seguenti relazioni:

$(f_1+f_2):f_1=(m_1+m_2):m_1 \; \; \rightarrow \; \; 2a:f_1=2c:m_1 \; \; \rightarrow \; \; m_1/f_1=c/a$

$(f_1+f_2):f_2=(m_1+m_2):m_2 \; \; \rightarrow \; \; 2a:f_2=2c:m_2 \; \; \rightarrow \; \; m_2/f_2=c/a$

Quindi i triangoli $H_1PF_1$ e $F_1PN$ sono simili (avendo lo stesso angolo $\alpha$ e due angoli alterni interni).
Analogamente sono simili anche i triangoli $H_2PF_2$ e $F_2PN$ .

Quindi si possono scrivere le proporzioni

$m_1:f_1=f_1:d_1=c/a$

da cui segue che

$f_1:d_1=f_2:d_2=c/a \; \rightarrow \; f_1=(c/a) \cdot d_1; \; \; \; \; \; f_2=(c/a) \cdot d_2$

ovvero

$\overline{PF_1}=e\cdot \overline{PH_1}; \; \; \; \; \; \overline{PF_2}=e\cdot \overline{PH_2}$

Per completare la dimostrazione è necessario mostrare che i punti $H_1$ e $H_2$ si trovano su due rette parallele ovvero che la distanza tra questi due punti sia indipendente dalla scelta del punto $P$ appartenente all’ellisse.
Queste due rette sono le due possibili per la direttrice, una alla destra e una alla sinistra del segmento formato dai due fuochi.

Dapprima si può osservare che il segmento $H_1H_2$ è, per costruzione, parallelo all’asse focale $F_1F_2$ e che i due punti $H_1$ e $H_2$ sono simmetrici rispetto all’asse del segmento $F_1F_2$ .

In aggiunta, si può verificare che la distanza $\overline{H_1H_2}=d_1+d_2$ è costante.
In fatti la proporzione $f_1:f_2=d_1:d_2$ può essere riscritta come

$(d_1+d_2):d_2=(f_1+f_2):f_2$

e dato che $f_1+f_2=2a$ , $d_2/f_2=a/c$ e che $d_1+d_2=\overline{H_1H_2}$ segue che

$(d_1+d_2)=2a \cdot d_2/f_2 \rightarrow (d_1+d_2)=2a \cdot (a/c)\rightarrow\overline{H_1H_2}=2a \cdot (a/c)$

Pertanto la distanza $\overline{H_1H_2}$ non dipende dalla scelta del punto $P$ sull’ellisse e la distanza della direttrice dall’asse verticale dell’ellisse è $a^2/c=a/e$ .

Questo completa la dimostrazione che $\overline{PF_1}=e\cdot \overline{PH_1}$ (o $\overline{PF_2}=e\cdot \overline{PH_2}$ ) e che $\overline{PH_1}$ (o $\overline{PH_2}$ ) è la distanza di $P$ da una opportuna retta fissa (direttrice) che è perpendicolare alla retta passante per i due fuochi $F_1$ e $F_2$ come si voleva appurare¹.

¹ Il fatto che la direttrice (luogo in cui si trovano i punti $H_1$ ) sia una retta perpendicolare all’asse focale segue dal fatto che la seconda direttrice (luogo dei punti $H_2$ ) è per costruzione simmetrica alla prima rispetto all’asse del segmento $F_1F_2$ e dal fatto che le distanze $\overline{H_1H_2}$ sono costanti. Solo una retta perpendicolare all’asse focale soddisfa entrambe le condizioni.

II) Seconda parte: B) $\rightarrow$ A)

Dato il luogo dei punti ( $P$ ) del piano per per cui il rapporto tra le distanze da un punto dato $F_1$ (fuoco) e da una retta data $d$ (direttrice) mantiene un valore costante $e$ con $0<e<1$ , allora

II.1) Esiste un secondo fuoco $F_2$ e una seconda direttrice $d_2$ per i quali vale la stessa relazione tra le loro distanze con $P$ , ovvero $\overline{PF_2}/\overline{Pd_2}=e=\text{costante}$ .

II.2) Per ogni punto $P$ dell’ellisse la somma delle distanze di $P$ dai due fuochi $F_1$ e $F_2$ si mantiene costante.

Dimostrazione di II.1

In pratica, partendo dal fuoco $F_1$ , dalla direttrice $d_1$ e da un punto $P$ del luogo, chiamando $H_1$ la proiezione di $P$ sulla direttrice si costruisce il $PF_1H_1$ e il triangolo simile $PF_1N$ in cui il lato $F_1N$ è parallelo alla retta $PH_1$ e avente l’angolo $F_1 \overhat{P} N$ congruente all’angolo $F_1 \overhat{H_1}P$ del primo triangolo. Si chiami $V$ il punto di intersezione tra le rette $PN$ e $H_1F_1$ . Il secondo fuoco $F_2$ , sulla retta $FN$ , è tale che la retta $PV$ sia bisettrice dell’angolo $F_2\widehat{P}F_1$ .

La retta $VF_2$ interseca la retta $H_1P$ nel punto $H_2$ che definisce la posizione della seconda direttrice $d_2$ (ovvero la retta passante per $H_2$ parallela a $d_1$ ).

fig. 2: costruzione dell’ellisse dalla definizione “fuoco-direttrice” (costruzione parziale)

Con la costruzione realizzata fino a questo punto è possibile mostrare che il triangolo $VF_1F_2$ è isoscele.

Infatti i triangoli $H_1PF_1$ e $PF_1N$ sono simili (per costruzione).
I triangoli $PF_2N$ e $F_1VN$ sono anch’essi simili, dato che hanno due angoli congruenti: $F_1 \widehat NV = F_2 \widehat NP$ (angoli opposti al vertice) e che $N \widehat F_1V=N \widehat P F_2$ ( $N \widehat F_1 V=P \widehat H_1F_1=N \widehat P F_2$ ).
Quindi vale la proporzione $\overline{PN}:m_2=m_1:\overline{NV}$ .

Anhe i triangoli $PF_1N$ e $NF_2V$ sono simili, per il secondo criterio di similitudine (o, con terminologia inglese, per il SAS similarity criterion), dato che essi hanno un angolo congruente, $P \widehat NF_1=F_2 \widehat NV$ (angoli opposti al vertice) e dato che per i due lati che formano tali angoli vale la proporzione precedentemente ricavata $\overline{PN}:m_2=m_1:\overline{NV}$ (o anche $\overline{PN}:m_1=m_2:\overline{NV}$ ).

Quindi $V \widehat F_1N=F_1 \widehat P N=F_1 \widehat P N=N \widehat F_2V$ e questo completa la dimostrazione che il triangolo $F_1VF_2$ è isoscele.
Ne consegue che $\overline{F_1V}=\overline{F_2V}$ e che il punto $V$ si trova sull’asse del segmento $F_1F_2$ .
Inoltre si può facilmente mostrare che $F_1 \widehat PF_2+F_1 \widehat VF_2=F_1 \widehat PF_2+F_1 \widehat V F_2=180^\circ$ e questo implica il fatto che il quadrilatero $PF_1VF_2$ è un quadrilatero ciclico e che il punto $V$ appartiene alla circonferenza circoscritta al triangolo $F_1PF_2$ .
Con la costruzione del punto $H_2$ si può ricavare che anche i triangoli $NPF_2$ e $PF_2H_2$ sono simili (per la congruenza degli angoli alterni interni $P \widehat F_2 N=F_2 \widehat P H_2$ e per la congruenza degli angoli $N \widehat P F_2=P \widehat H_2 F_2$ che deriva dalla costruzione effettuata.

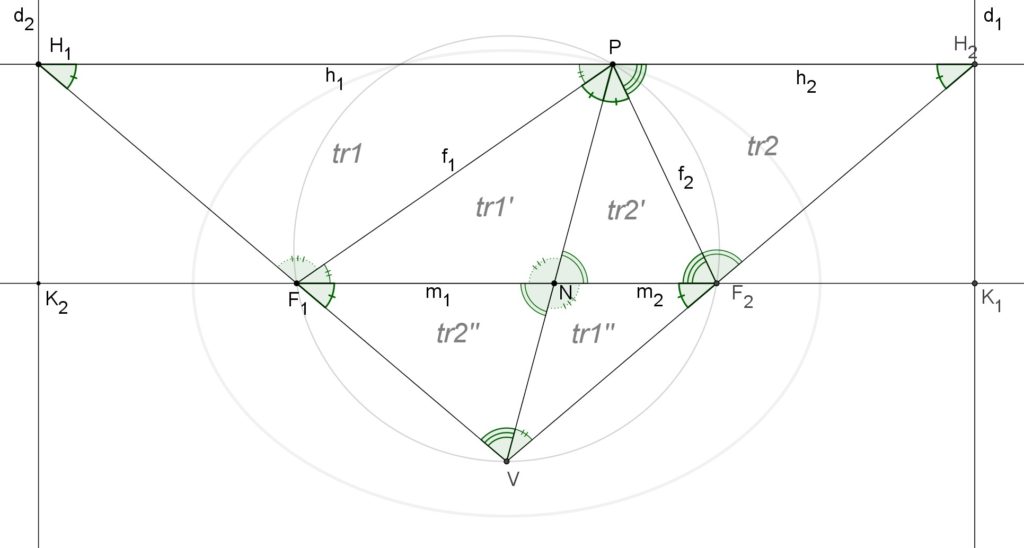
Nella figura sottostante (fig. 3) sono riportate le relazioni geometriche fin qui ricavate e gli angoli tra loro congruenti (aventi lo stesso simbolo). Sono inoltre evidenziate le similitudini dei triangoli $tr1,\;tr1',\;tr1''$ , quelle dei triangoli $tr2,\;tr2',\;tr2''$ .

Ellipse construction from focus-directrix

fig. 3: relazioni geometriche nella costruzione dell’ellisse dalla definizione fuoco-direttrice

Per il teorema della bisettrice applicato al triangolo $PF_1F_2$ , dove l’angolo $\widehat P$ è suddiviso nei due angoli congruenti $F_1 \widehat{P} N$ and $N \widehat{P} F_2$ , vale la proporzione

(a) $f_1:m_1=f_2:m_2$

Per la similitudine dei triangoli $H_1PF_1$ e $PF_1N$ è

(b) $m_1:f_1=f_1:h_1$

Per la similitudine dei triangoli $H_2PF_2$ e $PF_2N$ è

Unendo le proporzioni (a) e (b) con la proporzione (c) è

$f_1:h_1=f_2:h_2$

ovvero

$\overline{PF_1}/\overline{PH_1}= \overline{PF_2}/\overline{PH_2}=e$

Dimostrazione di II.2

Dato che

$f_1:d_1=f_2:d_2=e$

segue che

$f_1=e\cdot d_1$

and

$f_2=e\cdot d_2$

e sommando i termini delle due eguaglianze si ricava

$f_1+f_2=e \cdot (d_1+d_2)=e \cdot \overline{H_1H_2}$

Pertanto si può affermare che la somma delle distanze di $P$ dai due fuochi $F_1$ e $F_2$ si mantiene costante.
Q.E.D.

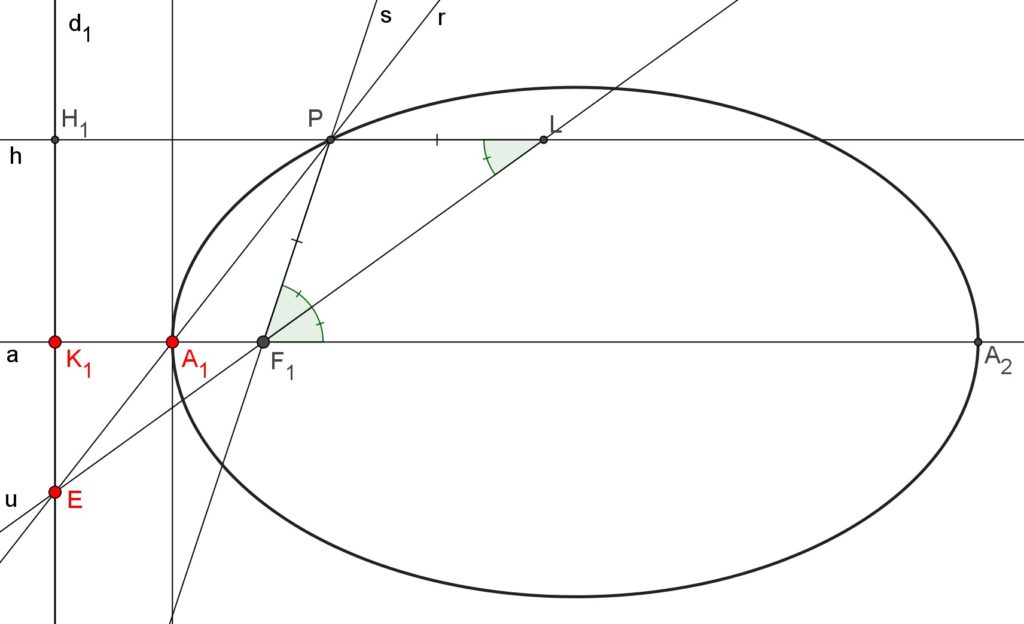
III) Costruzione geometrica dell’ellisse utilizzando la definizione B)

Per arricchire ulteriormente le relazioni geometriche insite nella definizione B) dell’ellisse riporto di seguito una delle possibili costruzioni geometriche (realizzabile con riga e compasso) dei punti $P$ che costituiscono l’ellisse.
La costruzione è tratta dal testo classico
W. H. Besant – Conic Sections Treated Geometrically – 1895 – capitolo 3
(si veda la sezione di riferimenti in fondo all’articolo per un collegamento al testo completo scaricabile gratuitamente).
Rispetto alla versione originale ho modificato i nomi di punti e rette e ho fornito qualche maggior dettaglio per chiarire alcuni passaggi.

La costruzione si sviluppa a partire da una retta data $d_1$ (la direttrice) , da un punto dato $F_1$ (un fuoco). Un generico punto $P$ dell’ellisse dovrà essere tale da soddisfare la relazione

(d) $\overline{PF_1}/ \overline{PH_1}=\text{costante}=e$

con $0<e<1$ e dove $H_1$ è la proiezione di $P$ sulla retta $d_1$ .

fig. 4: costruzione geometrica dell’ellisse tratta dal testo di W. H. Besant

Costruzione
Sia $F_1$ il fuoco, $d_1$ la direttrice, $a$ la retta perpendicolare a $d_1$ passante per $F_1$ e $K_1$ il punto di intersezione tra le rette $a$ e $d_1$ .

Sia poi $A_1$ un punto sul segmento $F_1K_1$ che lo suddivida in due parti il cui rapporto sia $\overline{F_1A_1}/\overline{A_1K_1}=e$ .

Il punto $A_1$ è uno dei punti dell’ellisse, dato che rispetta la condizione (d) e, in particolare, è uno dei suoi vertici.
Sia poi $A_2$ un altro punto di $a$ tale che valga la proporzione $\overline{F_1A_2}:\overline{K_1A_2}=\overline{F_1A_1}:\overline{K_1A_1}$ . Anche $A_2$ è quindi un punto dell’ellisse e un altro dei suoi vertici,

Si scelga un qualsiasi punto $E$ sulla direttrice $d_1$ , e si tracci la retta $u$ passante per $E$ e $F_1$ . Si tracci poi, da $F_1$ , una seconda retta $s$ (diversa da $a$ ) tale da formare con la retta $EF_1$ lo stesso angolo che $EF_1$ forma con la retta $a$ .
Sia poi $r$ la retta passante per $E$ e $A_1$ e si chiami $P$ il punto di intersezione tra le rette $s$ e $r$ .
Si conduca da $P$ la retta $h$ parallela ad $a$ e si chiami $H_1$ la sua intersezione con la direttrice $d_1$ e $L$ la sua intersezione con la retta $u$ .
Dato che, per costruzione, è $L\widehat{F_1}A_2=L\widehat{F_1}P$ e dato che $L\widehat{F_1}A_2=P\widehat{L}F_1$ (angoli alterni interni) ne segue che $L\widehat{F_1}P=P\widehat{L}F_1$ e che il triangolo $PLF_1$ è isoscele.
Quindi è $\overline{PL}=\overline{PF_1}$ .
Considerando poi che $h$ e $a$ sono due rette parallele intercettate dalle rette $r$ , $u$ e $d_1$ , tutte passanti per il punto $E$ , per il teorema di Talete si può dire che

$\overline{A_1F_1}:\overline{A_1K_1}=\overline{PL}:\overline{PH_1}=e$

e utilizzando la congruenza tra $\overline{PL}$ e $\overline{PF_1}$ è anche

$\overline{A_1F_1}:\overline{A_1K_1}=\overline{PF_1}:\overline{PH_1}=e$

Pertanto il punto $P$ appartiene al luogo dei punti per i quali è $\overline{PF_1}:\overline{PH_1}=e=\text{costante}$ .
Se si modifica la scelta del punto $E$ su $d_1$ si ottiene un diverso punto $P$ , ma comunque, valendo anche per questo la relazione (d), anch’esso appartiene alla stessa ellisse.

Riferimenti

Pagine in italiano:

https://it.wikipedia.org/wiki/Ellisse
https://it.wikipedia.org/wiki/Sfere_di_Dandelin
https://it.wikipedia.org/wiki/Sezione_conica

Pagine in inglese:

https://en.wikipedia.org/wiki/Ellipse
https://en.wikipedia.org/wiki/Dandelin_spheres
https://en.wikipedia.org/wiki/Conic_section
https://www.physicsforums.com/threads/ellipse-geometric-equivalence-of-two-definitions.247417/
W. H. Besant – Conic Sections Treated Geometrically (1895) – (free ebook in Project Gutenberg)

worlds of math & physics

I segreti dell’ellisse: dimostrazione geometrica dell’equivalenza delle sue due definizioni

I) Prima parte: A) $\rightarrow$ B)

II) Seconda parte: B) $\rightarrow$ A)

III) Costruzione geometrica dell’ellisse utilizzando la definizione B)

Riferimenti

Ultima modifica: 11 ottobre 2016

I) Prima parte: A) B)

II) Seconda parte: B) A)

III) Costruzione geometrica dell’ellisse utilizzando la definizione B)

Riferimenti

Ultima modifica: 11 ottobre 2016

I) Prima parte: A) $\rightarrow$ B)

II) Seconda parte: B) $\rightarrow$ A)