potrebbe interessarti anche:
INTRODUZIONE
Qualche esercizio di calcolo combinatorio può proporre domande del tipo: “se si lanciano due dadi qual’è la la probabilità che la somma dei numeri delle due facce sia 9?”
La risposta non è particolarmente difficile se si enumerano i casi che soddisfano il particolare evento richiesto (somma=9), dividendo poi tale numero di “eventi favorevoli” per il numero dei “casi possibili“.
Ma come affrontare lo stesso tipo di problema se si vuole calcolare la probabilità, ad esempio, di ottenere la somma 31 lanciando 10 dadi? In questo caso il conteggio dei casi favorevoli per enumerazione richiederebbe un tempo davvero molto lungo!
In casi come quest’ultimo è possibile ricavare una formula generale che fornisca la probabilità di avere una qualsiasi somma p lanciando un qualsiasi numero di n dadi?
Cercando di trovare una risposta a questa domanda generale ho fatto qualche ricerca nel campo del calcolo combinatorio e ho riportato in questo articolo i risultati ottenuti.
Ma prima di affrontare il nocciolo della questione è opportuno chiarire le definizioni, la notazione e la terminologia utilizzata nel resto del documento.
PARTE 1:
Definizioni, simboli e richiami di calcolo combinatorio
Nel calcolo combinatorio esistono regole, convenzioni e simboli diversi utilizzati per indicare gli stessi concetti matematici.
In questa sezione sono riportate le notazioni e la terminologia utilizzati in questo articolo. In alcuni casi saranno anche citate terminologie alternative, sopratutto quelle derivate dalla tradizione e dalla letteratura anglosassone.
TERMINI GENERALI
Un insieme (set) è una collezione (non ordinata) di oggetti distinti.
La cardinalità |S| di un insieme S è il numero di elementi dell’insieme.
Un sottoinsieme (subset) è una parte dell’insieme. Ciò significa che B è un sottoinsieme di A se esso è contenuto in A, cioè se tutti gli elementi di B sono anche elementi di A.
Un multiinsieme (multiset) è una generalizzazione del concetto di insieme. Un multiinsieme può essere definito come un collezione di elementi che ammette componenti ripetuti. Il numero di volte in cui un elemento è ripetuto nel multiinsieme è la molteplicità di quell’elemento. La cardinalità di un multiinsieme è Il numero totale di elementi del multiinsieme (dove si contano più volte gli elementi ripetuti), e si ottiene sommando le molteplicità degli elementi che lo compongono.
Ad esempio nel multiinsieme M={a, a, b, b, b, c, d, d, d, d} le molteplicità degli elementi a, b, c e d sono rispettivamente 2, 3, 1 and 4, e la cardinalità |M| del multiinsieme è 10.
Se l’insieme A è costituito dagli elementi a, b, c, d, questo può essere definito indicando questi elementi distinti tra parentesi graffe: A={d, b, c, a}.
[Nota: l’ordine degli elementi riportati non ha alcun valore, per cui {d, a, c, b}, {c, b, a, d} e {a, b, c, d} sono lo stesso insieme]
L’insieme B={a, d, c} può essere considerato un sottoinsieme (proprio) di A.
A partire dagli stessi elementi a, b, c, d si potrebbero poi costruire infiniti multiinsiemi. Ad esempio {a, a, a, c, c, d, d, d, d, b} o {c, c, b, d, d, a, b, c}.
Si sottolinea ancora che negli insiemi, nei sottoinsiemi e nei multiinsiemi l’ordine degli elementi non conta.
Al contrario, se si vuole indicare una sequenza ordinata di oggetti o elementi, in cui conta l’ordine, si usano i termini successione, elenco, lista o tupla. Ad esempio la successione di numeri naturali (7, 5, 1, 4) è diversa dalla successione (1, 7, 5, 4).
1) PERMUTAZIONI
Una permutazione (permutation) è una sequenza ordinata degli n elementi di un insieme.
1.A) Il numero di possibili diverse permutazioni di n oggetti distinti appartenenti a un insieme S (permutazioni semplici) è:
![]()
Infatti ci sono n modi di scegliere l’oggetto che occupa la prima posizione, per ciascuno di essi ci sono n–1 modi di scegliere l’oggetto che occupa la seconda posizione, poi per ogni coppia di oggetti fissati nelle prime due posizioni ci sono n–2 modi di scegliere l’oggetto nella terza posizione, e così via, fino ad occupare tutte le posizioni.
Ad esempio ci sono ![]() diverse permutazioni dell’insieme di lettere ELANO:
diverse permutazioni dell’insieme di lettere ELANO:
ELANO, ELAON, ELNAO, ELNOA, ELOAN, ELONA, EALNO, EALON, EANLO, EANOL, EAOLN, EAONL, ENLAO, ENLOA, ENALO, ENAOL, ENOLA, ENOAL, EOLAN, EOLNA, EOALN, EOANL, EONLA, EONAL, LEANO, LEAON, LENAO, LENOA, LEOAN, LEONA, LAENO, LAEON, LANEO, LANOE, LAOEN, LAONE, LNEAO, LNEOA, LNAEO, LNAOE, LNOEA, LNOAE, LOEAN, LOENA, LOAEN, LOANE, LONEA, LONAE, AELNO, AELON, AENLO, AENOL, AEOLN, AEONL, ALENO, ALEON, ALNEO, ALNOE, ALOEN, ALONE, ANELO, ANEOL, ANLEO, ANLOE, ANOEL, ANOLE, AOELN, AOENL, AOLEN, AOLNE, AONEL, AONLE, NELAO, NELOA, NEALO, NEAOL, NEOLA, NEOAL, NLEAO, NLEOA, NLAEO, NLAOE, NLOEA, NLOAE, NAELO, NAEOL, NALEO, NALOE, NAOEL, NAOLE, NOELA, NOEAL, NOLEA, NOLAE, NOAEL, NOALE, OELAN, OELNA, OEALN, OEANL, OENLA, OENAL, OLEAN, OLENA, OLAEN, OLANE, OLNEA, OLNAE, OAELN, OAENL, OALEN, OALNE, OANEL, OANLE, ONELA, ONEAL, ONLEA, ONLAE, ONAEL, ONALE
1.B) Se gli elementi che vengono ordinati nella successione sono elementi di un multiinsieme, in cui possono esserci elementi ripetuti, le diverse sequenze che si possono formare con questi elementi sono le permutazioni con ripetizione.
il numero delle diverse permutazioni distinte (che differiscono tra loro per l’ordine degli elementi del multiinsieme) è
![]()
dove n è la cardinalità del multiinsieme e ![]() sono le molteplicità dei diversi elementi del multiinsieme (sarà quindi
sono le molteplicità dei diversi elementi del multiinsieme (sarà quindi ![]() ).
).
Tale numero di permutazioni con ripetizione viene anche chiamato coefficiente multinomiale (multinomial coefficient) ed è indicato con il simbolo ![]() .
.
La formula sopra riportata deriva dal fatto che, in questo caso, le permutazioni semplici degli elementi di un multiinsieme (con alcuni elementi ripetuti) possono dar luogo ad identiche sequenze che devono però essere conteggiate una sola volta. Ad esempio, le permutazioni della serie di cinque lettere “ELELL” forniscono soltanto 10 risultati distinti:
EELLL, ELELL, ELLEL, ELLLE, LEELL, LELEL, LELLE, LLEEL, LLELE, LLLEE
dato che, ad esempio le 6 permutazioni delle 3 L nelle prime tre posizioni danno luogo alla stessa sequenza. Pertanto
![]() .
.
Un tipico esempio dell’uso delle permutazioni con ripetizione è quello di contare il numero dei differenti anagrammi di una parola con qualche lettera ripetuta. Ad esempio il numero dei possibili anagrammi della parola di 6 lettere “pioppo” (che ha 3 “p“, 2 “o” e 1 “i“) è
![]() .
.
2) DISPOSIZIONI
2.A) Le disposizioni semplici di n elementi di classe k (k-permutations) sono le possibili sequenze ordinate di k elementi distinti estratti da un insieme S di n elementi.
Pertanto, diversamente dalle permutazioni semplici, qui non è più necessario inserire nelle sequenze tutti gli n elementi di S.
In questo senso le disposizioni semplici possono essere considerate una generalizzazione del concetto di permutazione semplice. Infatti, nel caso particolare in cui k sia uguale a n, le disposizioni semplici coincidono con le permutazioni semplici.
Le disposizioni semplici possono essere anche viste anche come tutte le possibili permutazioni degli elementi di tutti quei sottoinsiemi di S aventi cardinalità k.
Sono considerate disposizioni semplici diverse quelle sequenze che differiscono se presentano qualche elemento diverso o se presentano gli stessi elementi ma in ordine diverso.
Il numero di disposizioni semplici di di n elementi di classe k è:
![]() .
.
Infatti ci sono n diverse possibilità per la scelta del primo elemento, n-1 possibilità per la scelta del secondo (dato che uno degli n elementi è già stato utilizzato), n-2 possibilità per la scelta del terzo (dato che due elementi sono già stati utilizzati) e così via fino al k-esimo elemento.
Ad esempio ci sono ![]() possibili ordini di arrivo dei primi tre cavalli in una corsa con 8 partecipanti.
possibili ordini di arrivo dei primi tre cavalli in una corsa con 8 partecipanti.
2.B ) Se si rimuove la condizione che i k elementi facenti parte della sequenza siano distinti, ovvero se si ammettono possibili ripetizioni di alcuni elementi, si hanno le “disposizioni con ripetizione“ di n elementi di classe k . Nelle disposizioni con ripetizione può essere ![]() .
.
Il numero di possibili diverse disposizioni con ripetizione è:
![]()
Infatti in questo caso, essendo permesse le ripetizioni dello stesso elemento, avremo n diverse possibilità per la scelta del primo elemento, n possibilità per la scelta del secondo, n possibilità per la scelta del terzo e così via fino al k-esimo elemento.
Ad esempio ci sono ![]() disposizioni con ripetizione formate da due lettere prese dall’insieme di tre lettere {a, b, c}: aa, ab, ac, ba, bb, bc, ca, cb, cc.
disposizioni con ripetizione formate da due lettere prese dall’insieme di tre lettere {a, b, c}: aa, ab, ac, ba, bb, bc, ca, cb, cc.
3) COMBINAZIONI
Una combinazione è una selezione di elementi presi da un insieme in cui, a differenza delle disposizioni, l’ordine non conta.
3.A) COMBINAZIONI SEMPLICI (O COMBINAZIONI SENZA RIPETIZIONI)
Se le ripetizioni di qualcuno degli elementi selezionati non sono ammesse una combinazione semplice di k elementi presi da un insieme S di n elementi (chiamata combinazione di n elementi di classe k) è un sottoinsieme di S, avente cardinalità k. Nelle combinazioni senza ripetizione deve essere ![]() .
.
Dato che l’ordine degli elementi non conta, due elenchi di oggetti con gli stessi elementi ma con ordinamenti diversi sono considerati la stessa combinazione.
Il numero di possibili combinazioni di n elementi di classe k è dato dalla formula
![]()
dove il simbolo ![]() (n su k) è chiamato coefficiente binomiale.
(n su k) è chiamato coefficiente binomiale.
La formula corrisponde alla divisione tra il numero delle disposizioni semplici di n oggetti di classe k e il numero delle possibili permutazioni dei k oggetti. Infatti nelle disposizioni (dove l’ordine conta) ogni diverso sottoinsieme di k oggetti viene contato ![]() volte, ovvero una volta per ogni diversa possibile permutazione. Ma dato che nelle combinazioni l’ordine non conta, queste
volte, ovvero una volta per ogni diversa possibile permutazione. Ma dato che nelle combinazioni l’ordine non conta, queste ![]() permutazioni corrispondono ad una singola combinazione e devono essere contate una sola volta. Questo si ottiene dividendo il numero di disposizioni
permutazioni corrispondono ad una singola combinazione e devono essere contate una sola volta. Questo si ottiene dividendo il numero di disposizioni ![]() per il numero di permutazioni
per il numero di permutazioni ![]() .
.
Un possibile esempio dell’uso di questa formula è quello di contare il numero di diverse squadre di pallacanestro (di 5 giocatori) che si possono formare da una rosa di 9 giocatori:
![]() .
.
3.B) COMBINAZIONI CON RIPETIZIONE
Se le ripetizioni sono consentite una combinazione con ripetizione di k elementi presi da un insieme S di n elementi è un raggruppamento di lunghezza k in cui ogni elemento può essere ripetuto fino a k volte. Ad esempio se S è l’insieme delle 4 lettere {a, b, c, d} alcune diverse combinazioni con ripetizione di classe 3 sono: {a, a, c}, {a, c, d}, {c, c, c}, … È importante osservare che anche in questo caso l’ordine non conta, per cui i raggruppamenti {a, a, c} e {a, c, a} sono considerati la stessa combinazione con ripetizione.
Una combinazione con ripetizione di n oggetti di classe k è quindi un multiinsieme di cardinalità k i cui elementi provengono da un insieme S di cardinalità n.
Dato che alcuni elementi possono essere ripetuti, nelle combinazioni con ripetizione può essere ![]() .
.
Il numero di possibili combinazioni con ripetizione di classe k (ovvero il numero di multiinsiemi di cardinalità k di un insieme di cardinalità n) è:
![]() .
.
Il simbolo ![]() viene chiamato coefficiente di multiinsieme (multiset coefficient).
viene chiamato coefficiente di multiinsieme (multiset coefficient).
Esempio 1: abbiamo acquistato 3 “palline” di gelato e possiamo scegliere tra 5 diversi gusti: banana, cioccolato, limone, stracciatella and vaniglia. Quanti sono i possibili tipi di gelato che possiamo avere? Usando le iniziali per i diversi gusti {b, c, l, s, v} alcuni possibili esempi di diversi gelati sono:
{c, c, c}: 3 palline tutte di cioccolato
{b, l, v}: una di banana, una di limone e una di vaniglia
{c, s, s}: una di cioccolato e due di stracciatella.
È quindi possibile scegliere più palline con lo stesso gusto ed è inoltre abbastanza evidente che l’ordine di scelta dei gusto non conta: il gelato {c, s, s} e il gelato {s, c, s} sono la stessa cosa.
Quindi in questo esempio ci sono n=5 possibili scelte (gusti), dobbiamo selezionare k=3 elementi da queste 5 possibilità (potendo anche ripetere uno degli elementi), e l’ordine di selezione degli elementi non conta. Siamo quindi in presenza di un caso tipico di combinazioni con ripetizione.
Applicando la formula sopra riportata Il numero di possibili diversi gelati che possiamo avere è:
![]() .
.
Esempio 2: Un altro significativo e classico esempio per l’utilizzo delle combinazioni con ripetizione è quello riconducibile a una richiesta del tipo “trova il numero di possibili modi di distribuire 3 biglie in 5 scatole“.
Questo esempio rientra nella categoria più generale di problemi che richiedono di individuare il numero di modi in cui si possono distribuire k oggetti, indistinguibili tra loro (biglie, palline, penne, magliette bianche…), in n contenitori.
In questo tipo di problema si assume implicitamente che, dopo la distribuzione, un contenitore possa anche risultare vuoto oppure contenere più di un oggetto (anche tutti).
Inoltre il numero totale dei k oggetti da distribuire nei contenitori può essere maggiore, uguale o minore del numero n dei contenitori.
La formula che fornisce la risposta alla domanda sul numero di possibili modi di distribuire 3 biglie in 5 scatole è:
![]() .
.
Abbiamo ottenuto lo stesso risultato del problema dei diversi tipi di gelato. Infatti entrambi i problemi hanno la stessa struttura se si considera la corrispondenza “scatole ![]() gusti” e “biglie
gusti” e “biglie ![]() palline di gelato“.
palline di gelato“.
In questo modo “una biglia in una scatola” può anche significare che la scatola (o l’associato gusto di gelato) è stata scelta; inoltre una scatola può contenere da 0 a 3 biglie (ovvero gusto non scelto o scelto per 1, 2, o 3 palline di gelato).
L’analogia si basa quindi sul fatto che una biglia in una scatola può essere pensata come un indicatore di scelta della scatola.
Nell’applicazione della formula delle combinazioni con ripetizione è importante capire cos’è n e cos’è k:
n rappresenta il numero delle cose che si possono (potenzialmente) scegliere (gusti di gelato o scatole) mentre k è il numero di scelte che si possono fare (palline di gelato) o di oggetti da distribuire (biglie), considerando anche che gli oggetti da distribuire nei contenitori possono essere pensati come indicatori di scelta dei contenitori.
Dato che qui, diversamente alle combinazioni semplici, è possibile che sia ![]() , varianti agli esempi precedentemente riportati potrebbero essere quelle di contare il numero di diversi gelati che si possono avere scegliendo 5 palline di gelato da 3 soli gusti o quello di contare il numero di modi in cui si possono distribuire 5 biglie in 3 scatole. In questo caso la formula è sempre valida ma bisogna però porre n=3 e k=5 e il risultato è diverso:
, varianti agli esempi precedentemente riportati potrebbero essere quelle di contare il numero di diversi gelati che si possono avere scegliendo 5 palline di gelato da 3 soli gusti o quello di contare il numero di modi in cui si possono distribuire 5 biglie in 3 scatole. In questo caso la formula è sempre valida ma bisogna però porre n=3 e k=5 e il risultato è diverso:
![]() .
.
Alcune note sulle combinazioni con ripetizione e giustificazione della formula
Dato che le combinazioni con ripetizione avranno un ruolo importante nella seconda parte di questo articolo vale la pena di comprendere meglio quale sia il loro significato e come nasca la formula riportata precedentemente.
La formula per il numero di possibili combinazioni con ripetizione di n oggetti di classe k
![]()
può essere spiegata, facendo riferimento al problema delle “3 biglie distribuite in 5 scatole”, nel seguente modo.
Per prima cosa assegniamo un particolare simbolo alle 3 biglie (ad esempio “⊕”) e un altro simbolo ai separatori delle scatole (ad esempio “|” ). Si noti che per creare 5 scatole sono sufficienti 4 separatori (e, in generale, per n scatole bastano n-1 separatori).
Con queste assegnazioni si può interpretare una qualsiasi sequenza dei simboli precedentemente definiti come una possibile distribuzione delle biglie nelle scatole. Ad esempio la sequenza |⊕||⊕|⊕⊕ rappresenta la distribuzione “0 biglie nella prima scatola; 1 biglia nella seconda; 0 biglie nella terza; 1 biglia nella quarta; 2 biglie nella quinta”, mentre la sequenza ⊕⊕ ||||⊕ rappresenta la distribuzione “2 biglie nella prima scatola; 1 biglia nella quinta scatola”.
Ogni possibile distribuzione delle 3 biglie nelle 5 scatole può così essere tradotta in una corrispondente sequenza dei due simboli e ogni diversa sequenza dei due simboli può rappresentare una diversa distribuzione delle biglie nelle scatole.
Il problema della distribuzione delle 3 biglie nelle 5 scatole può quindi essere tradotto nel problema di trovare il numero di diverse permutazioni con ripetizione di 2 simboli, che devono formare una sequenza di lunghezza 7.
In questo esempio un simbolo (⊕, biglia) deve essere ripetuto 3 volte e l’altro (|, separatore) 4 volte.
Si tratta quindi di determinare il numero di multiinsiemi di cardinalità 7 che possono essere formati con due elementi di molteplicità 3 e 4.
Questi multiinsiemi possono anche essere visti come i possibili anagrammi di una parola di lunghezza 7, in cui si possono utilizzare le due sole lettere ⊕ and | (la prima 3 volte e la seconda 4 volte).
Pertanto si può dire che ![]() e che, nel caso generale,
e che, nel caso generale, ![]() .
.
Successivamente questo concetto sarà utilizzato per determinare il numero di modi in cui (ad esempio) 10 dadi possono generare una somma di 31 punti. In questo ultimo caso si tratterà di determinare il numero di possibili distribuzioni dei 31 punti (biglie) tra 10 dadi (scatole).
PARTE 2:
Il problema di ottenere una certa somma lanciando più dadi
Origine del problema: un semplice esempio
Per rispondere alla domanda: “Se si lanciano due dadi qual è la probabilità di ottenere la somma 9?” dobbiamo prima definire lo spazio campionario U (insieme di tutti i possibili risultati che si possono ottenere):

In questo esempio, quindi, lo spazio campionario contiene 36 elementi (36 possibili esiti).
Dobbiamo poi determinare lo spazio degli eventi (insieme di tutti i sottoinsiemi di U).
Il particolare evento “la somma dei due dadi è 9” è il seguente elemento E dello spazio degli eventi: ![]() che contiene 4 membri.
che contiene 4 membri.
Se i due dadi non sono truccati ogni possibile esito di U può essere considerato ugualmente probabile, con probabilità 1/36 e la probabilità dell’evento E si può ottenere come rapporto tra la cardinalità di E e quella di U: ![]() ovvero come rapporto tra il numero degli esiti favorevoli e quello degli esiti possibili, considerando questi ultimi equiprobabili.
ovvero come rapporto tra il numero degli esiti favorevoli e quello degli esiti possibili, considerando questi ultimi equiprobabili.
Nota : Un possibile errore potrebbe essere quello di considerare l’evento E composto da coppie non ordinate di esiti: ![]() . In questo caso dovremmo anche considerare lo spazio campionario come composto da coppie non ordinate di esiti:
. In questo caso dovremmo anche considerare lo spazio campionario come composto da coppie non ordinate di esiti:

Con questa definizione di U lo spazio campionario conterrebbe ora 21 elementi invece dei precedenti 36, ma dire che ![]() sarebbe una risposta sbagliata.
sarebbe una risposta sbagliata.
La causa di questo errore deriva dal fatto che ora gli elementi dello spazio campionario non sono più ugualmente probabili. Infatti, nel lancio di due dadi, gli esiti che presentano due numeri diversi hanno una probabilità doppia di presentarsi rispetto a quelli con un singolo numero ripetuto due volte.
Si potrebbero aggiustare le cose dando un peso 2 agli esiti con numeri diversi e un peso 1 a quelli con il doppio numero. In questo modo la probabilità cercata diventerebbe![]() , ristabilendo il risultato corretto.
, ristabilendo il risultato corretto.
Generalizzazione
Nel precedente esempio è stato possibile determinare il numero di casi possibili dell’evento E (somma dei due dadi uguale a 9) per enumerazione.
Trovare che tale numero di esiti favorevoli è 4 (ovvero ![]() ) non ha richiesto molto tempo.
) non ha richiesto molto tempo.
Il denominatore (numero di casi possibili ![]() ) è stato calcolato direttamente con la formula delle disposizioni con ripetizione di 2 elementi presi da un insieme di 6 elementi.
) è stato calcolato direttamente con la formula delle disposizioni con ripetizione di 2 elementi presi da un insieme di 6 elementi.
Ma cosa succede se si vuole determinare la probabilità di ottenere (ad esempio) una somma di 31 con un lancio di 10 dadi?
In questo caso il denominatore (numero di casi possibili) potrà ancora essere determinato in modo semplice e diretto con la formula delle disposizioni con ripetizione: ![]() (servirà una calcolatrice), ma il numeratore? Quanto tempo ci vorrà per elencare e contare tutti i possibili esiti del lancio dei 10 dadi che producono una somma di 31? Uno dei possibili casi favorevoli potrebbe essere {6,3,4,3,5,2,1,1,2,4}, la cui somma è 31, ma è facile intuire che questo è solo uno tra tantissimi altri casi favorevoli che si potrebbero immaginare.
(servirà una calcolatrice), ma il numeratore? Quanto tempo ci vorrà per elencare e contare tutti i possibili esiti del lancio dei 10 dadi che producono una somma di 31? Uno dei possibili casi favorevoli potrebbe essere {6,3,4,3,5,2,1,1,2,4}, la cui somma è 31, ma è facile intuire che questo è solo uno tra tantissimi altri casi favorevoli che si potrebbero immaginare.
La domanda naturale è quindi: esiste una formula generale per determinare il numero dei possibili esiti favorevoli?
Tale formula dovrebbe permetterci di calcolare, in modo diretto, la probabilità di avere una certa somma ![]() lanciando
lanciando ![]() dadi, ciascuno con
dadi, ciascuno con ![]() facce (
facce (![]() nel caso di dadi comuni).
nel caso di dadi comuni).
La risposta è: sì, questa formula esiste:
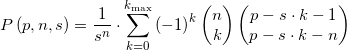 (1)
(1)
dove ![]() e
e ![]() è la funzione parte intera (floor function), che restituisce il numero intero più grande che è minore o uguale a x (ad esempio [6.83]=6).
è la funzione parte intera (floor function), che restituisce il numero intero più grande che è minore o uguale a x (ad esempio [6.83]=6).
Ho scoperto questa formula nella pagina http://mathworld.wolfram.com/Dice.html ma non sono riuscito a trovare nella rete qualche giustificazione intuitiva della sua particolare struttura.
In realtà la pagina di mathworld contiene una derivazione della formula, ma questa è però basata più su metodi algebrici che su un ragionamento fondato sui procedimenti tipici del calcolo combinatorio. Per questo motivo la dimostrazione presentata da mathworld e altre similari che si possono trovare nel web non hanno del tutto soddisfatto la mia l’esigenza di raggiungere una più approfondita comprensione della formula e della sua forma.
La formula (1) sopra riportata contiene alcune caratteristiche curiose, con il suo uso di segni alternati nella sommatoria e con l’uso della funzione parte intera.
Perché? Qual è l’origine di queste particolarità che non si trovano normalmente in altre formule del calcolo combinatorio?
Incuriosito da queste peculiarità ho cercato di capire meglio la struttura e la logica interna della formula, cercando di ricondurla ai concetti più classici del calcolo combinatorio.
La parte seguente di questa pagina descrive il percorso che ho seguito.
Verso una maggiore comprensione della formula
Per prima cosa proviamo ad applicare la formula al caso concreto di determinare la probabilità di ottenere la somma 31 con un lancio di 10 dadi.
Come visto in precedenza, qui la semplice elencazione e il conteggio del numero dei casi favorevoli non è praticabile (o richiederebbe un tempo molto lungo). È quindi necessario ricavare questo numero da un ragionamento più generale,
In questo esempio esplorativo consideriamo i comuni dadi cubici con 6 facce (s = 6). Inoltre p = 31, n = 10 e ![]() .
.
Quindi la formula (1) diventa:
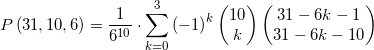
Possiamo ignorare il primo fattore ![]() (ovvero il numero degli esiti possibili utilizzato per calcolare la probabilità) e concentrarci sul secondo fattore (la sommatoria) che rappresenta il numero dei casi favorevoli, ovvero il numero degli esiti che producono sequenze diverse (anche solo per l’ordine) di 10 numeri da 1 a 6 la cui somma è 31. Chiamiamo questo numero
(ovvero il numero degli esiti possibili utilizzato per calcolare la probabilità) e concentrarci sul secondo fattore (la sommatoria) che rappresenta il numero dei casi favorevoli, ovvero il numero degli esiti che producono sequenze diverse (anche solo per l’ordine) di 10 numeri da 1 a 6 la cui somma è 31. Chiamiamo questo numero ![]() .
.
Se espandiamo la sommatoria otteniamo:
![]()
Per affrontare in termini generali il pfoblema del lancio dei dadi ho scelto il modello delle combinazioni con ripetizione che permette di risolvere problemi del tipo “trova il numero di possibili modi in cui si possono distribuire 3 biglie in 5 scatole” (ammettendo che al termine dell’operazione qualche scatola possa risultare vuota).
La formula delle combinazioni con ripetizione fornirebbe il risultato ![]() (si veda la precedente sezione “3.B Combinazioni con ripetizione“).
(si veda la precedente sezione “3.B Combinazioni con ripetizione“).
Perché questa scelta? Perché la formula delle combinazioni con ripetizione può essere applicata al problema del lancio di 10 dadi con somma 31 costruendo l’analogia biglie nelle scatole ![]() punti nei dadi.
punti nei dadi.
Nel caso dei dadi si tratterà quindi di determinare il numero dei modi in cui si possono distribuire 31 punti (biglie) in 10 scatole (dadi).
Qui il numero di elementi diversi tra cui scegliere (n) è 10 e corrisponde al numero dei dadi, mentre il numero di scelte che possiamo effettuare (k) è 31 e acquista il significato di attribuzione dei 31 punti ai 10 dadi (infatti ogni punto attribuito ad un dado può essere interpretato come scelta di quel dado):
![]() .
.
Il fatto che sia ![]() può sembrare strano dato che ciò non sarebbe possibile nel caso più comune delle combinazioni semplici. Ma, dato che qui le ripetizioni sono permesse nulla vieta di effettuare 31 scelte di 10 elementi diversi. Ad esempio se il 3° dado vale 4 questo può essere interpretato come se tale dado fosse stato scelto 4 volte e dovendo totalizzare un numero di 31 punti (scelte) con 10 elementi diversi (dadi) è inevitabile che ci siano ripetizioni.
può sembrare strano dato che ciò non sarebbe possibile nel caso più comune delle combinazioni semplici. Ma, dato che qui le ripetizioni sono permesse nulla vieta di effettuare 31 scelte di 10 elementi diversi. Ad esempio se il 3° dado vale 4 questo può essere interpretato come se tale dado fosse stato scelto 4 volte e dovendo totalizzare un numero di 31 punti (scelte) con 10 elementi diversi (dadi) è inevitabile che ci siano ripetizioni.
Seguendo lo stesso tipo di ragionamento fatto in precedenza nella sezione “Alcune note sulle combinazioni con ripetizione e giustificazione della formula” una spiegazione della formula ![]() consiste nel reinterpretarla tramite le permutazioni con ripetizione, usando il simbolo “|” a rappresentare un separatore tra due dadi e il simbolo “p” per rappresentare un punto assegnato a un dado.
consiste nel reinterpretarla tramite le permutazioni con ripetizione, usando il simbolo “|” a rappresentare un separatore tra due dadi e il simbolo “p” per rappresentare un punto assegnato a un dado.
Dato che per rappresentare 10 dadi bastano 9 separatori si tratterà allora di creare una sequenza di lunghezza 40 utilizzando 9 volte il simbolo “|” e 31 volte il simbolo “p”.
Ad esempio la sequenza
ppp|p|ppppp|pp|p|pppp|ppp|pppp|pppppp|pp
corrisponderebbe, nel lancio dei 10 dadi, all’esito {3,1,5,2,1,4,3,4,6,2} che ha somma 31.
Allo stesso tempo un qualsiasi esito del lancio di 10 dadi con somma 31 può essere tradotto in una sequenza di lunghezza 40 dei due simboli “|” e “p”.
Il numero di modi in cui si possono disporre in sequenza i 31 simboli “p” e i 9 simboli “|” non è altro che il numero di anagrammi di una parola di lunghezza 40 fatta con due sole lettere, una ripetuta 31 volte e l’altra 9 volte, ovvero ![]() .
.
Ma ora ci sono due problemi: il primo si può risolvere in modo abbastanza semplice ma il secondo è più complesso.
Entrambi nascono dal fatto che, diversamente dalle biglie nelle scatole (in cui una scatola può essere vuota o contenere qualche biglia o perfino contenerle tutte, lasciando le altre scatole vuote), qui a ogni dado si devono assegnare da un minimo di 1 punto (primo problema) a un massimo di 6 punti (secondo problema).
Soddisfare la prima condizione è facile. Basta assegnare d’ufficio un punto a ciascuno dei 10 dadi per un totale di 10 punti. Fatto ciò resteranno da assegnare 21 punti ai 10 dadi.
Se non ci fosse un limite massimo per il numero di punti da assegnare ad ogni dado (secondo problema) avremmo finito.
La formula delle combinazioni con ripetizione ci darebbe il numero delle possibili distribuzioni dei punti tra i dadi con ogni dado contenente da un minimo di 1 punto a un massimo di 22 punti (un dado conterrebbe 22 punti se, dopo il primo punto assegnato “a priori” ricevesse poi tutti gli altri 21 punti da distribuire):
![]()
Per verificare questo risultato proviamo ad applicare la formula generale (1) a dadi con un illimitato numero di facce. Nel nostro esempio è sufficiente considerare dadi con ![]() facce.
facce.
Con questa scelta di s ciascun dado potrebbe avere un valore compreso tra 1 e 22. Infatti, se dopo l’assegnazione preliminare di 1 punto a tutti i dadi un dado ricevesse tutti i restanti 21 punti da distribuire (lasciando gli altri 9 dadi a quota 1), questo dado avrebbe valore 22 (1+21) e, con gli atri 9 dadi (che danno un totale di 9 punti), si raggiungerebbe comunque il totale di 31.
Applicando la formula (1) a questo caso (con s=22, n=10 e p=31) si avrebbe ![]() e il numero delle possibili distribuzioni con un totale di 31 punti sarebbe:
e il numero delle possibili distribuzioni con un totale di 31 punti sarebbe:
![]() .
.
Questo è proprio il risultato ottenuto con le combinazioni con ripetizione ![]() .
.
Ciò significa che il metodo delle combinazioni con ripetizione è in accordo con la formula (1), almeno nel caso in cui si ignori il secondo problema relativo all’esistenza di un valore massimo di punti (6) che si possono assegnare ai dadi.
Il passo successivo è quello di modificare questo risultato temporaneo introducendo le correzioni necessarie per soddisfare il vincolo che che ogni dado reale può avere un valore massimo di 6.
Quindi, per determinare il numero corretto dei possibili esiti che possono presentare i comuni dadi a 6 facce, sarà necessario eliminare, dal numero dei possibili esiti determinati precedentemente con dati illimitati, il numero dei casi proibiti derivanti dai dadi fuorilegge che non rispecchiano il vincolo del valore massimo di 6 punti.
Considerando che, per rispettare il valore minimo di 1 punto per ogni dado, ogni dado ha già preliminarmente ricevuto 1 punto, il numero di nuovi punti che un dado legale potrà ricevere dovrà essere compreso tra 0 e 5. I dadi fuorilegge saranno quindi quelli che riceveranno (dopo la pre-assegnazione di 1 punto) un numero di punti ≥ 6.
Rimozione dei casi proibiti
Questa è la parte più difficile.
Si tratta di trovare un metodo per contare tutte le distribuzioni proibite, ovvero quelle in cui uno o più dadi hanno un valore ≥ 6. In tal modo potremo ottenere il numero di distribuzioni valide (o legali) tramite la sottrazione:
numero di distribuzioni valide = numero di distribuzioni con valori illimitati – numero di distribuzioni proibite.
Abbiamo già visto che il numero di distribuzioni con dadi illimitati è ![]() , quindi il problema su cui concentrare la nostra attenzione è quello di trovare il numero di distribuzioni proibite (quelle in cui uno o più dadi hanno un valore ≥ 6).
, quindi il problema su cui concentrare la nostra attenzione è quello di trovare il numero di distribuzioni proibite (quelle in cui uno o più dadi hanno un valore ≥ 6).
Innanzitutto consideriamo il caso in cui un dado è forzato ad essere un dado fuorilegge (con valore ≥6).
Per realizzare tale situazione possiamo pre-assegnare a un dado (ad esempio al dado 1) 6 punti. Dopo tale operazione resteranno 15 punti da distribuire a tutti i 10 dadi (questo significa che dopo l’assegnazione preliminare il dado 1 potrebbe ricevere altri punti e arrivare a un totale superiore a 6).
Utilizzando la formula delle combinazioni con ripetizione avremo:
![]()
Considerando però che che la scelta di rendere un singolo dado fuorilegge può avvenire in 10 modi diversi (10 possibili scelte del dado fuorilegge), il numero totale di distribuzioni proibite generate in questo modo sarà:
![]()
Chiamiamo questo gruppo di distribuzioni proibite ![]() (o gruppo “≥1sei”).
(o gruppo “≥1sei”).
La procedura sopra indicata potrebbe essere riassunta dai seguenti 4 passi eseguiti ciclicamente:
(1) si sceglie il primo dado
(2) si assegnano ad esso 6 punti
(3) si distribuiscono i rimanenti 15 punti a tutti i 10 dadi (incluso quello attualmente scelto come fuorilegge)
(4) si passa al dado successivo e si riparte dal passo (2)
Il ciclo terminerà dopo il raggiungimento del decimo dado.
È importante osservare che con l’assegnazione di 6 punti a un singolo dado (ad esempio il dado k) nel passo (2) e dei restanti 15 punti a tutti i 10 dadi nel passo (3) si possono verificare i seguenti casi:
a) dopo il passo (3) il dado k potrebbe ricevere altri punti e avere quindi un totale superiore a 6 (potrebbe perfino ricevere tutti gli altri punti da distribuire).
b) qualche altro dado ![]() potrebbe ricevere, nel passo (3), 6 o più punti e diventare così un altro dado fuorilegge anche se non forzosamente prescelto (nel passo (2)) per avere questa caratteristica.
potrebbe ricevere, nel passo (3), 6 o più punti e diventare così un altro dado fuorilegge anche se non forzosamente prescelto (nel passo (2)) per avere questa caratteristica.
A questo punto abbiamo costruito un gruppo di distribuzioni (![]() ) che include tutte le distribuzioni proibite con almeno 1 dado fuorilegge.
) che include tutte le distribuzioni proibite con almeno 1 dado fuorilegge.
Il numero di distribuzioni facenti parte di questo gruppo è:
![]()
Rimozione dei duplicati all’interno dei casi proibiti
Sfortunatamente c’è un problema nella procedura precedentemente descritta: nel gruppo ![]() (o gruppo “≥1sei”) delle distribuzioni con almeno un dado fuorilegge sono presenti duplicati.
(o gruppo “≥1sei”) delle distribuzioni con almeno un dado fuorilegge sono presenti duplicati.
In pratica il gruppo ![]() non è un insieme ma piuttosto un multiinsieme. Questo fatto può essere riconosciuto tramite un esempio.
non è un insieme ma piuttosto un multiinsieme. Questo fatto può essere riconosciuto tramite un esempio.
Supponiamo che il dado corrente prescelto per essere un dado fuorilegge sia il dado 2 e che quindi assegniamo ad esso 6 punti. Successivamente, dopo aver assegnato gli altri 15 punti ai 10 dadi e potremmo avere la seguente distribuzione (una tra le tante possibili): {1,6,0,4,0,0,3,1,6,0}.
Il totale dei punti assegnati in questo modo è 21 e il corrispondente risultato del lancio dei 10 dadi (considerando che 1 punto era stato precedentemente pre-assegnato ad ogni dado) sarebbe {2,7,1,5,1,1,4,2,7,1}, con somma 31 e due dadi fuorilegge.
Poi arriviamo al dado 9, assegniamo ad esso 6 punti e i restanti 15 punti ai 10 dadi. Potremmo allora avere (tra le altre) la stessa distribuzione {1,6,0,4,0,0,3,1,6,0}.
In pratica la stessa distribuzione di punti ai 10 dadi può essere prodotta e conteggiata due volte: una quando il dado 2 è forzato ad essere un dado fuorilegge e un’altra quando il dado 9 è forzato ad essere un dado fuorilegge.
La stessa cosa avviene ogniqualvolta ci sono due dadi fuorilegge nella distribuzione risultante.
Quindi, per trovare il numero di distribuzioni duplicate nel gruppo ![]() è necessario trovare il numero di distribuzioni aventi almeno 2 dadi fuorilegge.
è necessario trovare il numero di distribuzioni aventi almeno 2 dadi fuorilegge.
Chiameremo il gruppo con almeno 2 dadi fuorilegge gruppo ![]() (o gruppo “≥2sei”).
(o gruppo “≥2sei”).
Per costruire il gruppo ![]() possiamo pre-assegnare 6 punti a due dadi. Resteranno quindi 9 punti residui da ridistribuire poi ai 10 dadi e questo può essere fatto nel seguente numero di possibili modi:
possiamo pre-assegnare 6 punti a due dadi. Resteranno quindi 9 punti residui da ridistribuire poi ai 10 dadi e questo può essere fatto nel seguente numero di possibili modi:
![]() .
.
La scelta dei due dadi da rendere fuorilegge può però essere fatta in ![]() modi diversi; quindi il numero totale di distribuzioni proibite che vengono generate in questo modo è:
modi diversi; quindi il numero totale di distribuzioni proibite che vengono generate in questo modo è:
![]()
Ma anche in questo gruppo ci sono distribuzioni duplicate e anche questo gruppo è quindi un multiinsieme.
Infatti se i dadi con i 6 punti preassegnati fossero, ad esempio il dado 3 e il dado 7, distribuendo i restanti 9 punti potrebbe accadere che un altro dado, ad esempio il dado 9, diventi fuorilegge e un esempio specifico del risultato finale potrebbe essere la sequenza {1,0,6,0,0,0,6,2,6,0}.
Ma la stessa sequenza potrebbe essere prodotta non solo quando i due dati preassegnati sono il dado 3 e il dado 6 ma anche quando sono il dado 3 e il dado 9 e quando sono il dado 7 e il dado 9. Ci sono quindi ![]() sequenze duplicate per ogni doppia preassegnazione.
sequenze duplicate per ogni doppia preassegnazione.
Questo tipo di duplicazione avviene nel caso in cui ci siano, in totale, tre dadi fuorilegge nella distribuzione dei punti.
Quindi, per determinare i duplicati nel gruppo ![]() è necessario trovare il numero di distribuzioni aventi almeno 3 dadi fuorilegge.
è necessario trovare il numero di distribuzioni aventi almeno 3 dadi fuorilegge.
Chiamiamo questo gruppo ![]() .
.
Sembra non ci sia fine a questa continua necessità di trovare il numero di distribuzioni con sempre più dadi fuorilegge ma, fortunatamente ora le cose cambiano.
Infatti ci accorgiamo (con un certo sollievo) che non ci possono essere più di 3 dadi fuorilegge (con valore ![]() ) nelle distribuzioni cercate, se la somma dei 10 dadi deve essere 21.
) nelle distribuzioni cercate, se la somma dei 10 dadi deve essere 21.
Infatti 4 sei darebbero un totale di 24 che è maggiore del totale che si vuole ottenere.
Pertanto il gruppo ![]() non può contenere duplicati (è un insieme a tutti gli effetti e non un multiinsieme) e può essere denotato come gruppo “=3sei”.
non può contenere duplicati (è un insieme a tutti gli effetti e non un multiinsieme) e può essere denotato come gruppo “=3sei”.
Per trovare il numero di possibili sequenze del gruppo ![]() dobbiamo preassegnare 6 punti a 3 dadi diversi. Ci saranno ora solamente 3 punti residui da distribuire ai 10 dadi (e nessun altro dado potrà quindi diventare un nuovo dado fuorilegge) e il numero di possibili distribuzioni sarà:
dobbiamo preassegnare 6 punti a 3 dadi diversi. Ci saranno ora solamente 3 punti residui da distribuire ai 10 dadi (e nessun altro dado potrà quindi diventare un nuovo dado fuorilegge) e il numero di possibili distribuzioni sarà:
![]() .
.
Considerando che possiamo effettuare la scelta dei 3 dadi fuorilegge in ![]() modi diversi, il numero totale di distribuzioni proibite del gruupo “=3six” sarà :
modi diversi, il numero totale di distribuzioni proibite del gruupo “=3six” sarà :
![]() .
.
Dato che non ci possono essere più di 3 sei nella distribuzione dei punti ai dadi, nel gruppo ![]() non ci potranno essere sequenze duplicate e abbiamo finalmente raggiunto la fine del processo.
non ci potranno essere sequenze duplicate e abbiamo finalmente raggiunto la fine del processo.
È importante osservare che ci sono sequenze duplicate del gruppo ![]() non solo nel gruppo
non solo nel gruppo ![]() ma anche nel gruppo
ma anche nel gruppo ![]() . Infatti se il dado preassegnato a ricevere i 6 punti fosse il dado 6, dopo la distribuzione dei restanti 15 punti ci potrebbero essere altri due dadi fuorilegge, ad esempio il dado 3 e il dado 8.
. Infatti se il dado preassegnato a ricevere i 6 punti fosse il dado 6, dopo la distribuzione dei restanti 15 punti ci potrebbero essere altri due dadi fuorilegge, ad esempio il dado 3 e il dado 8.
Un esempio specifico di possibile distribuzione potrebbe essere la sequenza {1,1,6,0,0,6,0,6,0,1}. La stessa sequenza sarebbe conteggiata anche quando il dado preassegnato è il dado 3 e quando è il dado 8. Ci sono quindi ![]() sequenze duplicate per ogni preassegnazione di 1 sei a un dado. Queste sequenze appartengono sia al gruppo
sequenze duplicate per ogni preassegnazione di 1 sei a un dado. Queste sequenze appartengono sia al gruppo ![]() che al gruppo
che al gruppo ![]() che all’insieme
che all’insieme ![]() .
.
Possiamo finalmente procedere a ritroso per costruire il numero di distribuzioni proibite uniche, depurate dai casi duplicati.
Per far ciò è utile definire i seguenti numeri:
![]() : numero delle distribuzioni uniche con esattamente 3 sei;
: numero delle distribuzioni uniche con esattamente 3 sei;
![]() : numero delle distribuzioni uniche con esattamente 2 sei;
: numero delle distribuzioni uniche con esattamente 2 sei;
![]() : numero delle distribuzioni uniche con esattamente 1 sei;
: numero delle distribuzioni uniche con esattamente 1 sei;
Adottando tali definizioni possiamo dire che:
![]() è già formato da distribuzioni uniche con esattamente 3 sei e quindi
è già formato da distribuzioni uniche con esattamente 3 sei e quindi ![]() è la cardinalità di
è la cardinalità di ![]() :
:
![]() .
.
![]() include 3 volte le distribuzioni con esattamente 3 sei.
include 3 volte le distribuzioni con esattamente 3 sei.
Il numero di distribuzioni uniche con esattamente 2 sei si può ottenere sottraendo ![]() dalla cardinalità di
dalla cardinalità di ![]() :
:
![]()
![]() include 2 volte le distribuzioni uniche con esattamente due sei e 3 volte le distribuzioni uniche con esattamente 3 sei.
include 2 volte le distribuzioni uniche con esattamente due sei e 3 volte le distribuzioni uniche con esattamente 3 sei.
Quindi il numero di distribuzioni con esattamente 1 sei è:
![]()
Finalmente possiamo contare il numero delle possibili distribuzioni proibite, senza distribuzioni duplicate:
![]()
![]()
Questo è il numero di distribuzioni (uniche) che contengono 1 o 2 o 3 sei.
La figura seguente visualizza il numero di sequenze duplicate nei gruppi ![]() ,
, ![]() e
e ![]() e il risultato ottenuto
e il risultato ottenuto ![]() .
.
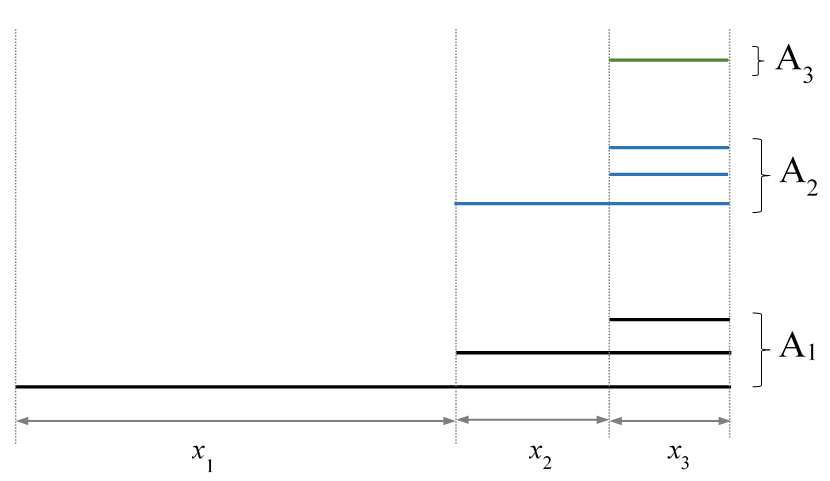 Figura 1: Il gruppo
Figura 1: Il gruppo ![]() include tutte le distribuzioni con esattamente 1 sei (conteggiate una volta) ma anche le distribuzioni con 2 sei (conteggiate 2 volte) e quelle con 3 sei (conteggiate 3 volte).
include tutte le distribuzioni con esattamente 1 sei (conteggiate una volta) ma anche le distribuzioni con 2 sei (conteggiate 2 volte) e quelle con 3 sei (conteggiate 3 volte).
Allo stesso modo il gruppo ![]() include tutte le distribuzioni con esattamente 2 sei (conteggiate 1 volta) ma anche quelle con 3 sei (conteggiate 3 volte).
include tutte le distribuzioni con esattamente 2 sei (conteggiate 1 volta) ma anche quelle con 3 sei (conteggiate 3 volte).
In generale nel multiinsieme ![]() le distribuzioni con esattamente j sei sono conteggiate
le distribuzioni con esattamente j sei sono conteggiate ![]() volte.
volte.
Lo stesso risultato può anche essere derivato algebricamente risolvendo il seguente sistema nelle incognite ![]() ,
, ![]() e
e ![]() :
:
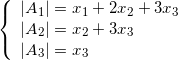
che ha soluzioni:
![]()
da cui si ricava
![]()
La figura seguente mostra la struttura annidata delle inclusioni e delle sequenze duplicate dei gruppi ![]() .
.
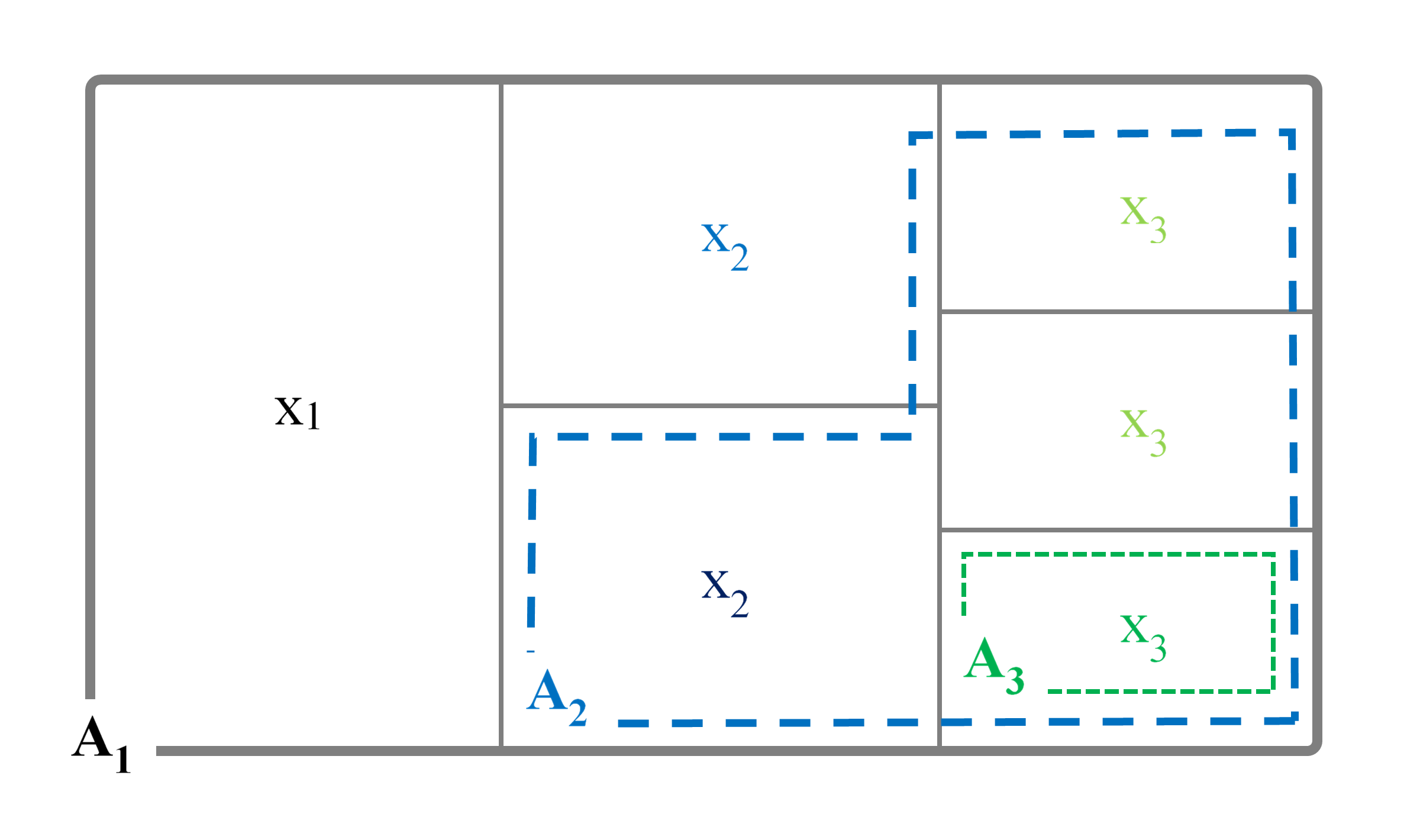 Figura 2: Un’altra rappresentazione grafica della struttura dei multiinsiemi
Figura 2: Un’altra rappresentazione grafica della struttura dei multiinsiemi ![]() e
e ![]() e dei loro elementi duplicati, da cui si può verificare visivamente come si possano ottenere le sequenze proibite uniche
e dei loro elementi duplicati, da cui si può verificare visivamente come si possano ottenere le sequenze proibite uniche ![]() tramite le formule
tramite le formule ![]() .
.
Conclusioni per il caso del lancio di 10 dadi con somma 31
Dopo aver trovato il numero di distribuzioni proibite e dopo aver depurato questo numero dalle distribuzioni duplicate possiamo finalmente applicare la relazione
numero di distribuzioni permesse = numero di distribuzioni con dadi illimitati – numero di distribuzioni proibite
dove il numero di distribuzioni con dadi illimitati è:
![]()
il numero di distribuzioni proibite (senza duplicati) è:
![]()
![]()
e il numero delle distribuzioni permesse è quindi:
![]()
![]()
in accordo con la formula generale (1).
Concretamente, considerando il numero di possibili esiti (![]() ), possiamo affermare che la probabilità di avere una somma di 31 punti con un lancio di 10 dadi è:
), possiamo affermare che la probabilità di avere una somma di 31 punti con un lancio di 10 dadi è:
![]()
Inoltre si può verificare che il massimo valore di probabilità per una certa somma si ottiene per un totale di 35 punti (7.269%), che la probabilità di avere una somma compresa tra 30 e 40 (estremi inclusi) è 68.699% e che la probabilità di avere una somma compresa tra 25 e 45 (estremi inclusi) è 94.950%.
Conclusioni per la formula generale
Al termine del lungo procedimento per costruire l’espressione che fornisce la probabilità di ottenere una somma di 31 punti con un lancio di 10 dadi, espressione che, come abbiamo verificato, è in accordo con la formula generale (1), abbiamo acquisito una migliore comprensione sul ruolo dei diversi elementi che costituiscono la formula.
Ad esempio la funzione parte intera (floor function) è legata al fatto che nei casi proibiti non ci possono essere più di 3 sei se si vuole avere una somma di 31 punti (21 punti da distribuire più i 10 punti preassegnati) e i segni alternati nascono dal processo di rimozione delle distribuzioni duplicate dai multiinsiemi ![]() (mentre
(mentre ![]() è un insieme e non ha elementi duplicati) per ottenere il vero insieme delle distribuzioni proibite (senza duplicati), la cui cardinalità è
è un insieme e non ha elementi duplicati) per ottenere il vero insieme delle distribuzioni proibite (senza duplicati), la cui cardinalità è ![]() .
.
La tecnica usata per rimuovere i casi duplicati è basata sul principio di inclusione ed esclusione, anche se, nel caso analizzato in questa pagina, abbiamo dovuto affrontare la complicazione aggiuntiva di doverlo applicare a multiinsiemi e non a semplici insiemi.
Approfondimento: una interpretazione duale
Per ottenere il numero di distribuzioni con dadi illimitati abbiamo usato le combinazioni con ripetizione: ![]() e abbiamo detto che questa formula ha il significato di contare il numero di possibili modi di distribuire 21 punti tra dieci dadi.
e abbiamo detto che questa formula ha il significato di contare il numero di possibili modi di distribuire 21 punti tra dieci dadi.
Ma dato che ![]() avremmo ottenuto lo stesso risultato anche usando le combinazioni con ripetizione
avremmo ottenuto lo stesso risultato anche usando le combinazioni con ripetizione ![]()
(In generale ![]() ).
).
Le combinazioni con ripetizione ![]() possono essere interpretate come il numero di possibili modi di distribuire 9 dadi tra 22 gradini di una scalinata, numerati da 0 a 21.
possono essere interpretate come il numero di possibili modi di distribuire 9 dadi tra 22 gradini di una scalinata, numerati da 0 a 21.
Se ordiniamo i dadi in sequenza sulla base della loro altezza lungo la scalinata (dal più basso al più alto), Il numero associato al gradino i occupato dal k-esimo dado rappresenta la somma cumulata dei dadi da 1 a k.
Ad esempio, se il gradino con valore 13 è occupato dal dado 3 (e i dadi 1 e 2 si trovano in gradini più bassi), ciò vuol dire che la somma dei valori dei dadi 1, 2 e 3 è 13. Inoltre il valore del dado 3 sarà pari alla differenza tra il numero del gradino in cui è collocato il dado 3 e quello del gradino in cui è collocato il dado 2.
Il 10° dado non viene considerato nella formula delle combinazioni con ripetizione perché è assegnato “d’ufficio” al 22° gradino (che ha numero 21), garantendo così un totale della somma dei valori dei dadi pari a 21.
Pertanto le combinazioni con ripetizione ![]() (9 dadi nei 22 gradini di una scalinata) possono essere messe in corrispondenza biunivoca con le combinazioni con ripetizione
(9 dadi nei 22 gradini di una scalinata) possono essere messe in corrispondenza biunivoca con le combinazioni con ripetizione ![]() (21 punti collocati in 10 scatole). In entrambi i casi un dado può avere un valore da 0 (due dadi nello stesso gradino o una scatola vuota) a 21 (ad esempio 9 dadi nel primo gradino di numero 0 con il 10° dado virtuale nel gradino di numero 21 oppure tutti i 21 punti collocati nella 10° scatola).
(21 punti collocati in 10 scatole). In entrambi i casi un dado può avere un valore da 0 (due dadi nello stesso gradino o una scatola vuota) a 21 (ad esempio 9 dadi nel primo gradino di numero 0 con il 10° dado virtuale nel gradino di numero 21 oppure tutti i 21 punti collocati nella 10° scatola).
Il corrispondente coefficiente binomiale ![]() associato alle combinazioni con ripetizione
associato alle combinazioni con ripetizione ![]() suggerisce di interpretare questo numero come conteggio delle combinazioni semplici di 9 diversi elementi (simboli) presi da un insieme di 30 diversi simboli.
suggerisce di interpretare questo numero come conteggio delle combinazioni semplici di 9 diversi elementi (simboli) presi da un insieme di 30 diversi simboli.
Nel nostro caso i 30 diversi simboli possono essere semplicemente i numeri naturali da 1 a 30 e ![]() è il numero di possibili estrazioni di 9 numeri dall’urna che contiene i 30 numeri.
è il numero di possibili estrazioni di 9 numeri dall’urna che contiene i 30 numeri.
Dato che nelle combinazioni l’ordine non conta, ogni possibile singola combinazione può essere rappresentata con la sequenza dei 9 numeri estratti disposti in ordine crescente.
Una delle possibili combinazioni potrebbe ad esempio essere: {5,11,17,22,23,24,26,28,29}.
Questa sequenza potrebbe anche essere interpretata come la somma cumulata dei punti dei dadi dopo il lancio di 9 dadi. La combinazione sopra riportata potrebbe quindi essere associata al seguente esito del lancio dei 9 dadi: {5,6,6,5,1,1,2,2,1}.
Dato che in realtà i dadi da lanciare sono 10 (e non 9) e che la somma dei 10 dadi deve essere 31 (e non 29), possiamo semplicemente aggiungere il numero 31 al termine della sequenza dei 9 numeri naturali.
In questo modo ogni lancio di 10 dadi con somma 31 può essere rappresentato da una sequenza ordinata di lunghezza 9 dei 30 numeri naturali da 1 a 30 con il numero 31 aggiunto al termine della lista.
Analogamente, ogni sequenza ordinata di lunghezza 9 dei 30 numeri naturali da 1 a 30 con il numero 31 aggiunto al termine della lista può essere tradotta nell’esito di un lancio di 10 dadi con somma 31. Esiste quindi una corrispondenza biunivoca tra i possibili esiti del lancio di 10 dadi con somma 31 e le sequenze ordinate costruite come specificato sopra.
È importante osservare che lanci di dadi che presentano gli stessi valori ma con diverse distribuzioni tra i 10 dadi sono rappresentati da diverse sequenze di numeri.
Ad esempio l’esito del lancio di 10 dadi {3,5,2,2,5,4,1,1,2,6} è rappresentato dalla sequenza {3,8,10,12,17,21,22,23,25,31}. Se invertissimo i valori dei dadi 1 e 2 avremmo il diverso esito {5,3,2,2,5,4,1,1,2,6} che è associato alla diversa sequenza di numeri {5,8,10,12,17,21,22,23,25,31} (cioè a una diversa combinazione).
È giusto che sia così dato che per calcolare la probabilità di una certa somma dobbiamo conteggiare i due esiti sopra riportati come esiti diversi (si veda il caso dei due dadi con somma 9 descritto sopra nella sezione Origine del problema: un semplice esempio) anche se i valori prodotti dai 10 dadi sono gli stessi.
Questa interpretazione duale sembra più semplice di quella presentata precedentemente in questo articolo: infatti in questo caso la condizione che che ogni dado debba contribuire con almeno un punto alla somma non necessita nessun aggiustamento artificiale ed è automaticamente soddisfatta dal fatto che due numeri naturali consecutivi presenti nella lista ordinata differiscono sempre di almeno una unità.
Ad ogni modo anche l’interpretazione duale non risolve il problema dei dadi fuorilegge (quelli con valori superiori a 6).
Ad esempio la sequenza di numeri {1,3,12,15,16,18,20,21,29,31} sarebbe tradotta in un esito proibito del lancio dei 10 dadi: {1,2,9,3,1,2,2,1,8,2} con due dadi fuorilegge.
Con questa interpretazione duale una distribuzione proibita avviene ogniqualvolta nella sequenza dei 9 numeri naturali (con il numero 31 aggiunto alla fine) il primo numero o la differenza tra due elementi consecutivi è maggiore di 6.
Ma trovare il modo più semplice per rimuovere le sequenze proibite in questo nuovo scenario è un’altra storia…
Riferimenti
In italiano:
Wikipedia – Calcolo combinatorio: http://it.wikipedia.org/wiki/Calcolo_combinatorio
Wikipedia – Permutazione: http://it.wikipedia.org/wiki/Permutazione
Wikipedia – Disposizione: http://it.wikipedia.org/wiki/Disposizione
Wikipedia – Combinazione: http://it.wikipedia.org/wiki/Combinazione
Wikipedia – Permutazione: http://it.wikipedia.org/wiki/Permutazione
Wikipedia – Multiinsieme: http://it.wikipedia.org/wiki/Multinsieme
Wikipedia – Funzione parte intera: http://it.wikipedia.org/wiki/Parte_intera
Wikipedia – Principio di inclusione ed esclusione: http://it.wikipedia.org/wiki/Principio_di_inclusione_ed_esclusione
Wikipedia – Partizione di un intero: http://it.wikipedia.org/wiki/Partizione_di_un_intero
In inglese:
Mathworld – The dice roll problem and the general formula: http://mathworld.wolfram.com/Dice.html
Counting and Probability (Johan Claeys): http://home.scarlet.be/math/tel.htm
Notes on Probability and Statistics (Andrew Forrester, pdf): http://aforrester.bol.ucla.edu/educate/Math/Notes_Probability.pdf
Mathisfun – Combinations and Permutations: http://www.mathsisfun.com/combinatorics/combinations-permutations.html
Wikipedia – Permutation: http://en.wikipedia.org/wiki/Permutation
Wikipedia – Combination: http://en.wikipedia.org/wiki/Combination
Wikipedia – Multiset: http://en.wikipedia.org/wiki/Multiset
Wikipedia – Floor and ceiling functions: http://en.wikipedia.org/wiki/Floor_and_ceiling _functions
Wikipedia – Inclusion-exclusion principle: http://en.wikipedia.org/wiki/Inclusion–exclusion_principle
Wikipedia – Partition (number theory): http://en.wikipedia.org/wiki/Partition_(number_theory)