La via “trigonometrica” a E=mc²

[scarica il pdf (in inglese): EMC2_rev01.pdf]

In questa nota presentiamo la dimostrazione della famosa formula di Einstein E=m{{c}^{2}} partendo dalla definizione relativistica di quantità di moto: p=\frac{{{m}_{0}}v}{\sqrt{1-{{{v}^{2}}}/{{{c}^{2}}}\;}}.
Per far ciò applicheremo lo stesso procedimento utilizzato per arrivare alla definizione di energia cinetica nella dinamica classica.

Consideriamo un corpo avente massa {{m}_{0}} che, partendo da fermo, raggiunge una certa velocità v. L’energia acquisita dal corpo è definita come il lavoro fatto per far raggiungere al corpo la velocità finale v.

W=\int{Fdx=\int{\frac{dp}{dt}dx=}}\int{vdp} dato che v=\frac{dx}{dt}

Nella dinamica Newtoniana la quantità di moto è p={{m}_{0}}v per cui, assumendo che la massa del corpo non cambi, è

W=\int{vdp}=\int{vd\left( {{m}_{0}}v \right)}={{m}_{0}}\int{vdv=\frac{1}{2}{{m}_{0}}{{v}^{2}}}

Questa è la definizione di energia cinetica (kinetic energy – KE) acquisita dal corpo.

Nella relatività speciale dobbiamo però usare una diversa espressione per la quantità di moto:

p=\frac{{{m}_{0}}v}{\sqrt{1-{{{v}^{2}}}/{{{c}^{2}}}\;}}=\gamma {{m}_{0}}v dove \gamma ={{\left( 1-{{{v}^{2}}}/{{{c}^{2}}}\; \right)}^{{-\,1}/{2}\;}}

Si può osservare che, per preservare la precedente definizione di quantità di moto mv, è possibile definire una nuova quantità, chiamata massa relativistica m=\gamma {{m}_{0}} diversa dalla massa a riposo m_0 e dire che la massa relativistica è la massa di un corpo avente velocità v. Tale concetto di massa relativistica è comunque controverso e soggetto a possibili fraintendimenti.

Quindi l’integrale da calcolare con l’espressione relativistica della quantità di moto è

W=\int{vdp}=\int{v\frac{d}{dv}\left( \gamma {{m}_{0}}v \right)dv}

Procederemo al calcolo in due modi diversi: a) con una sostituzione, usando la funzione goniometrica seno per il rapporto {v}/{c}\; e b) senza sostituzione, usando le usuali tecniche di integrazione e differenziazione .

a) La via “trigonometrica”

La via”trigonometrica” presentata nelle righe seguenti si presta a interessanti interpretazioni geometriche e rende il calcolo più semplice e veloce. È basata sulla semplice sostituzione:

\sin \alpha =\frac{v}{c}

da cui segue v=c\cdot \sin \alpha;   \gamma ={{\left( 1-\frac{{{v}^{2}}}{{{c}^{2}}} \right)}^{{-\,1}/{2}\;}}=\frac{1}{\sqrt{1-{{\sin }^{2}}\alpha }}=\frac{1}{\cos \alpha }

e

p=\gamma {{m}_{0}}v={{m}_{0}}c\frac{\sin \alpha }{\cos \alpha }={{m}_{0}}c\tan \alpha

Con queste nuove espressioni l’integrale diventa:

W=\int{c\cdot \sin \alpha \cdot d\left( {{m}_{0}}c\tan \alpha \right)}={{m}_{0}}{{c}^{2}}\int{\left( \sin \alpha \right)d\left( \tan \alpha \right)={{m}_{0}}{{c}^{2}}}\int{\frac{\sin \alpha }{{{\cos }^{2}}\alpha }d\alpha }

E l’integrazione è quasi immediata:

W={{m}_{0}}{{c}^{2}}\int{\frac{\sin \alpha }{{{\cos }^{2}}\alpha }d\alpha }={{m}_{0}}{{c}^{2}}\left[ \frac{1}{\cos \alpha } \right]_{0}^{\alpha }={{m}_{0}}{{c}^{2}}\left( \frac{1}{\cos \alpha }-1 \right)

Tornando alle grandezze originarie abbiamo:

W=KE={{m}_{0}}{{c}^{2}}\left( \gamma -1 \right)=\gamma {{m}_{0}}{{c}^{2}}-{{m}_{0}}{{c}^{2}}=m{{c}^{2}}-{{m}_{0}}{{c}^{2}}

Quindi l’energia cinetica relativistica può essere pensata come la quantità di m{{c}^{2}} in eccesso rispetto alla quantità invariante {{m}_{0}}{{c}^{2}} che possiamo interpretare come energia a riposo.
 Inoltre si può scrivere

\underbrace{KE+{{m}_{0}}{{c}^{2}}}_{E}=m{{c}^{2}}

e questa equazione porta alla celebre formula di Einstein E=m{{c}^{2}} se si definisce E,  l’energia totale, come somma di energia cinetica (l’energia collegata alla sola velocità acquisita) e energia a riposo (energia collegata alla sola massa a riposo, {{m}_{0}}{{c}^{2}})

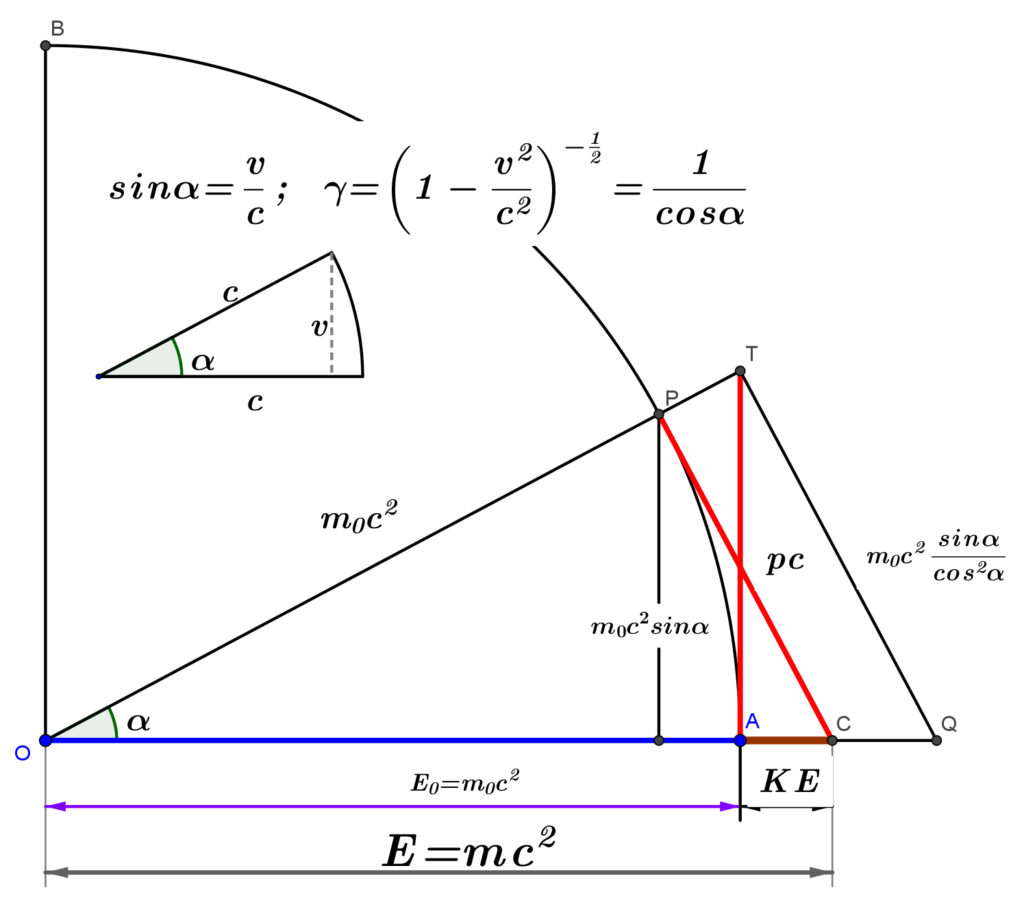
La figura seguente mostra le interessanti relazioni geometriche tra le principali grandezze coinvolte nel calcolo se si usa la sostituzione \sin \alpha =\frac{v}{c}

    \[{m_0}{c^2},\,\,\,\,pc = {m_0}{c^2}\tan \alpha ,\,\,\,\,{\rm K}{\rm E} = {m_0}{c^2}\left( {\frac{1}{{\cos \alpha }} - 1} \right), \,\,\,E = KE + {m_0}{c^2} = m{c^2} = {m_0}{c^2}\sec \alpha\]

In aggiunta, la figura mostra che l’importante relazione energia-quantità di moto

{{E}^{2}}={{\left( pc \right)}^{2}}+{{\left( {{m}_{0}}{{c}^{2}} \right)}^{2}}

deriva dalla semplice applicazione del teorema di Pitagora al triangolo OPC.

b) Integratione senza sostituzione

L’integrale

W=\int{vdp}=\int{v\frac{dp}{dv}dv}

può essere calcolato anche senza utilizzare la sostituzione trigonometrica.

Iniziamo con il calcolo del termine differenziale \frac{dp}{dv}:

\begin{array}{l} \frac{{dp}}{{dv}} = \frac{d}{{dv}}\left( {\gamma {m_0}v} \right) = {m_0}\frac{d}{{dv}}\left( {\frac{v}{{\sqrt {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} }}} \right) = {m_0}\frac{d}{{dv}}\left( {v{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{1}{2}}}} \right) = \\ = {m_0}\left( {{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{1}{2}}} + v\left( { - \frac{1}{2}} \right){{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{3}{2}}}\left( { - 2\frac{v}{{{c^2}}}} \right)} \right) = \end{array}

\begin{array}{l} = {m_0}\left( {{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{1}{2}}} + \left( {{{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right){{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{3}{2}}}} \right) = {m_0}{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)^{ - \frac{1}{2}}}\left( {1 + \left( {{{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right){{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - 1}}} \right) = \\ = {m_0}{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)^{ - \frac{1}{2}}}\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}} + {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right){\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)^{ - 1}} = {m_0}{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)^{ - \frac{1}{2}}}{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)^{ - 1}} = {m_0}{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)^{ - \frac{3}{2}}} \end{array}

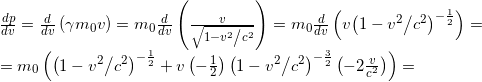
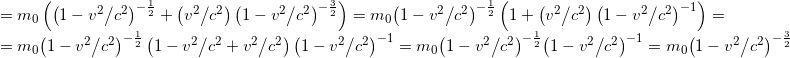
Ora possiamo procedere con il calcolo dell’integrale

    \[\begin{array}{l} W = \int {v\frac{{dp}}{{dv}}dv} = \int {v{m_0}{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{3}{2}}}dv} = - \frac{{{m_0}{c^2}}}{2}\left( { - 2} \right)\left[ {{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \,\frac{1}{2}}}} \right]_0^v = \\ = {m_0}{c^2}\left( {{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \,\frac{1}{2}}} - 1} \right) = {m_0}{c^2}\left( {\gamma - 1} \right) = m{c^2} - {m_0}{c^2} \end{array}\]

Alla fine abbiamo ottenuto, anche se in modo più faticoso, lo stesso risultato del calcolo con la sostituzione .

 

Ultima modifica: 2 giugno 2018

 

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *