Ellipse: geometric proof of the equivalence of two definitions

Every time I try to get some deeper insight about Newton’s gravitational law I stumble upon the geometrical properties of the ellipse.
After many years of these strange and challenging encounters I really think that the ellipse is a rich and wonderful trove of geometrical nuances and subtleties.

The geometric definition of an ellipse can be given with two alternative but equivalent statements:

A) An ellipse is a plane curve whose points ( $P$ ) are such that the sum of the distances from $P$ to two fixed points (the foci, $F_1$ and $F_2$ ) is constant. That is

$\overline {PF_1} + \overline {PF_2} = \text{const} = 2a$ (where $a$ is the semi-major axis of the ellipse)

B) An ellipse is a plane curve whose points ( $P$ ) are such that the ratio of the distance of $P$ from a fixed point (focus) $F_1$ and from a fixed line (directrix) $d_1$ is constant. That is, calling $H_1$ the perpendicular projection of $P$ on $d_1$ , it is

$\overline{PF_1}/ \overline{PH_1}= \text{const}=e$ (where $0<e<1$ )

The equivalence of the two definitions can be elegantly proved in space geometry (3D) with the Dandelin spheres, and using the fact that the ellipse is a conic section.
Another possible road is to use the analytic geometry in a Cartesian frame of reference.

Anyway I have been for a long time looking for a geometric proof of the equivalence of the two definitions using pure plane geometry (in 2D) using the classic procedures of Euclidean geometry.

Since I couldn’t find any proof of this kind in the web, some years ago (in 2008) I tried to devise one by myself.

By pure chance I’ve rediscovered in these days (October 2016) that old demonstration of several years ago and I’ve found it quite interesting and potentially rich of clues for other possible geometric investigations, although in need of some refinement.

So, here is a possible (and tentative) pure geometric demonstration using plain plane geometry showing the equivalence of the two definitions of the ellipse.
It is essentially unchanged with respect to the old version, but I have added a few more details to smooth out some passages.

I’m fully aware this demonstration is much more complex than the one with the Dandelin spheres, and that it could be improved and maybe made simpler, but it temporarily meets my needs for a proof living in plane (2D) geometry (until I find something better than this).

The first part I) is aimed to prove that definition A) implies definition B) while the second part II) (just sketched as it is mostly a reversion of the steps followed in the first part) is aimed to prove that definition B) implies A).
In a third part III) I’ve included a geometric construction of the ellipse, taken from a classic textbook.

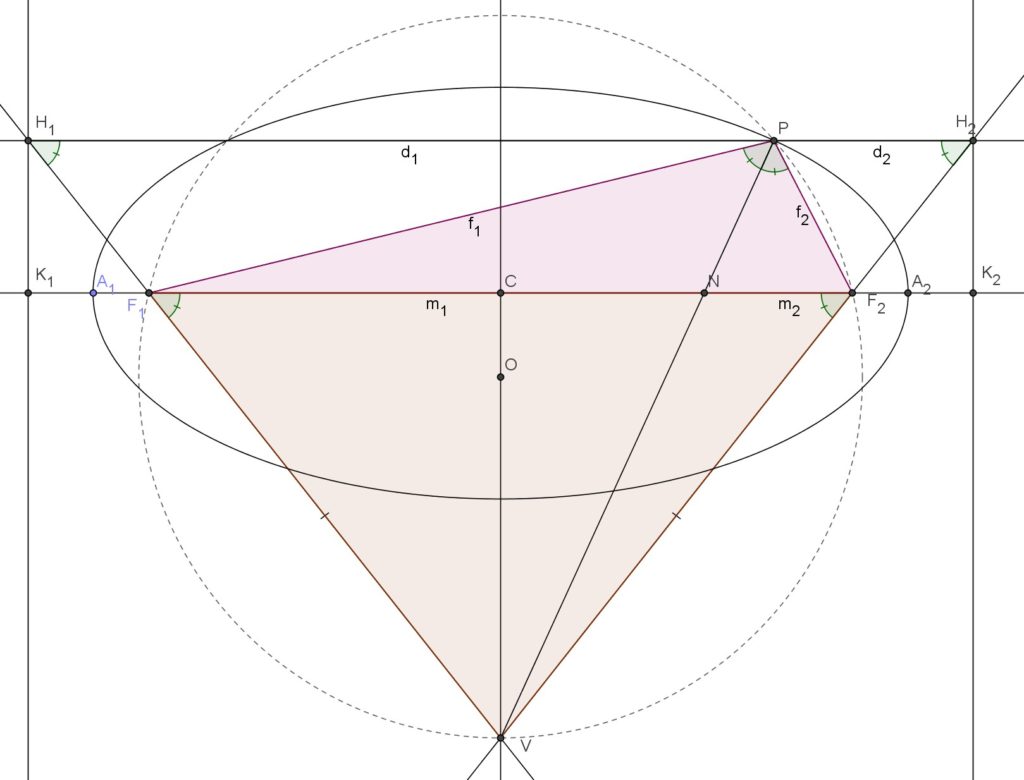
fig.1: equivalence of the “two foci” and “focus-directrix” definitions

I) First part: A) 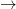$\rightarrow$ B)

Given the locus of points for which is constant the sum of the distances from two fixed points $F_1$ and $F_2$ then for any point $P$ belonging to the locus it is $\overline{PF_1}=e\cdot \overline{PH_1}$ , where $\overline{PH_1}$ is the distance from $P$ and an appropriate fixed line (directrix) perpendicular to the line joining $F_1$ and $F_2$ .

Demonstration

Let it be

$\overline{F_1F_2}=2c; \; \; \overline{PF_1}+\overline{PF_2}=2a; \; \; c/a=e; \; \; \overline{PF_1}=f_1; \; \; \overline{PF_2}=f_2$

First, consider the triangle $F_1F_2P$ , and construct the circumscribed circle around it.

The perpendicular bisector of the segment $F_1F_2$ meets the circle (on the arc $\stackrel {\frown} {F_1F_2}$ not including $P$ ) in $V$ . The quadrilateral $VF_1F_2P$ is then a cyclic quadrilateral.

Let’s call $N$ the intersection of the line $PV$ with the line joining $F_1$ and $F_2$ , and we’ll call $\overline{NF_1}=m_1$ and $\overline{NF_2}=m_2$ .

We also define $H_1$ and $H_2$ as the points where the line through $P$ and parallel to $F_1F_2$ meets the lines $VF_1$ and $VF_2$ respectively. We’ll then call $\overline{PH_1}=d_1; \; \; \overline{PH_2}=d_2$

Since $\overline{F_1V}=\overline{F_2V}$ , it follows, for the chord properties, that the segment $PV$ bisects the angle $F_1PF_2$ , so that $F_1\widehat{P}N=N\widehat{P}F_2=F_1\widehat{F_2}V=\alpha$

Applying the angle bisector theorem to the triangle $F_1PF_2$ we have

$f_1:m_1=f_2:m_2$

It’s also

$(f_1+f_2):f_1=(m_1+m_2):m_1 \; \; \rightarrow \; \; 2a:f_1=2c:m_1 \; \; \rightarrow \; \; m_1/f_1=c/a$

and

$(f_1+f_2):f_2=(m_1+m_2):m_2 \; \; \rightarrow \; \; 2a:f_2=2c:m_2 \; \; \rightarrow \; \; m_2/f_2=c/a$

The triangles $H_1PF_1$ and $F_1PN$ are similar (they have the same angle $\alpha$ and two alternate interior angles). So, also the triangles $H_2PF_2$ and $F_2PN$ are similar.

Thence it is

$m_1:f_1=f_1:d_1=c/a$

and

$m_2:f_2=f_2:d_2=c/a$

whence

$f_1:d_1=f_2:d_2=c/a \; \rightarrow \; f_1=(c/a) \cdot d_1; \; \; \; \; \; f_2=(c/a) \cdot d_2$

That is

$\overline{PF_1}=e\cdot \overline{PH_1}; \; \; \; \; \; \overline{PF_2}=e\cdot \overline{PH_2}$

To complete the demonstration we must show that the points $H_1$ and $H_2$ lie on two parallel lines that have a certain constant distance, independently of the choice of the point $P$ of the ellipse.
These two lines are the two alternative choices for the directrix, at the right or left side of the segment joining the two foci.

First, it can be observed that the line segment $H_1H_2$ is, by construction, parallel to the focal axis $F_1F_2$ and that the two points $H_1$ and $H_2$ are symmetric with respect to the perpendicular bisector of the segment $F_1F_2$ .

Furthermore, the distance $\overline{H_1H_2}=d_1+d_2$ is constant.
In fact the proportion $f_1:f_2=d_1:d_2$ can be rewritten as

$(d_1+d_2):d_2=(f_1+f_2):f_2$

and since $f_1+f_2=2a$ , $d_2/f_2=a/c$ and $d_1+d_2=\overline{H_1H_2}$ we have

$(d_1+d_2)=2a \cdot d_2/f_2 \rightarrow (d_1+d_2)=2a \cdot (a/c)\rightarrow\overline{H_1H_2}=2a \cdot (a/c)$

So the distance $\overline{H_1H_2}$ doesn’t depend on the choice of the point $P$ on the ellipse and the distance of the directrix line from the vertical axis of the ellipse is $a^2/c=a/e$ .

This completes the demonstration that $\overline{PF_1}=e\cdot \overline{PH_1}$ (or $\overline{PF_2}=e\cdot \overline{PH_2}$ ) and that $\overline{PH_1}$ (or $\overline{PH_2}$ ) is the distance from $P$ to an appropriate fixed line (directrix) perpendicular to the line joining $F_1$ and $F_2$ as for the initial statement¹.

¹ That the directrix is a straight line perpendicular to the focal axis follows from the fact that the second directrix is symmetric to the first with respect of the perpendicular bisector of the segment $F_1F_2$ and from the fact that the distances $\overline{H_1H_2}$ are constant. Only a straight vertical line satisfies both these conditions.

II) Second part: B) 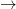$\rightarrow$ A)

Given the locus of points for which the ratio between the distances from a fixed point $F_1$ (focus) and a fixed line (directrix) has a constant value $e$ with $0<e<1$ , then

II.1) There exists a second focus $F_2$ and a second directrix $d_2$ for which the same relation between the distances from $P$ apply, That is $\overline{PF_2}/\overline{Pd_2}=e= \text{const}$ .

II.2) For any point $P$ belonging to the locus the sum of the distances of $P$ to the foci $F_1$ and $F_2$ has a constant value.

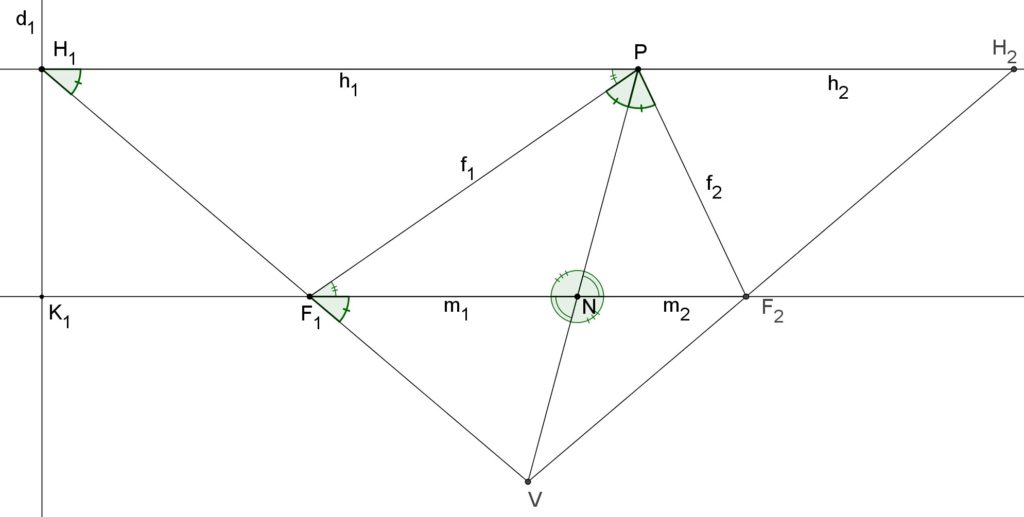
Demonstration of II.1

Basically, starting from the focus $F_1$ , the directrix $d_1$ , a point $P$ belonging to the locus, and calling $H_1$ the perpendicular projection of $P$ on the directrix it’s possible to build the triangle $PF_1H_1$ , and the similar triangle $PF_1N$ where the side $F_1N$ is parallel to $PH_1$ and with the angle $F_1 \overhat{P} N$ congruent to the angle $F_1 \overhat{H_1}P$ . The lines $PN$ and $H_1F_1$ meets at a point $V$ . The second focus $F_2$ , on the line $FN$ , is such that the line $PV$ bisects the angle $F_2\widehat{P}F_1$ . The line $VF_2$ intersects the line $H_1P$ in the point $H_2$ that defines the position of the second directrix $d_2$ (that is the line through $H_2$ parallel to $d_1$ ).

fig. 2: ellipse construction from the “focus-directrix” definition (partial)

With this construction we can show that the triangle $VF_1F_2$ is isosceles.

In fact, the triangles $H_1PF_1$ and $PF_1N$ are similar (by construction).
The triangles $PF_2N$ and $F_1VN$ are similar, since they have two congruent angles: $F_1 \widehat NV = F_2 \widehat NP$ (opposite angles) and $N \widehat F_1V=N \widehat P F_2$ ( $N \widehat F_1 V=P \widehat H_1F_1=N \widehat P F_2$ ).
Then it is $\overline{PN}:m_2=m_1:\overline{NV}$ .

Also the triangles $PF_1N$ and $NF_2V$ are similar, for the SAS similarity criterion, since they have a congruent angle, $P \widehat NF_1=F_2 \widehat NV$ (opposite angles) and the two sides adjacent to that angle have lengths in the same ratio. In fact, as shown above, it is $\overline{PN}:m_2=m_1:\overline{NV}$ (or, equivalently, $\overline{PN}:m_1=m_2:\overline{NV}$ ).

Then $V \widehat F_1N=F_1 \widehat P N=F_1 \widehat P N=N \widehat F_2V$ and this proves the fact that the triangle $F_1VF_2$ is isosceles.
Thence $\overline{F_1V}=\overline{F_2V}$ and the point $V$ belongs to the perpendicular bisector of the segment $F_1F_2$ .
Furthermore it can be easily proved that $F_1 \widehat PF_2+F_1 \widehat VF_2=F_1 \widehat PF_2+F_1 \widehat V F_2=180^\circ$ and that imply that the quadrilateral $PF_1VF_2$ is a cyclic quadrilateral and that the point $V$ belongs to the circumscribed circle of the triangle $F_1PF_2$ .
With the construction of the point $H_2$ we can see that also the triangles $NPF_2$ and $PF_2H_2$ are similar (for they have the congruent alternate interior angles $P \widehat F_2 N=F_2 \widehat P H_2$ and the congruent angles $N \widehat P F_2=P \widehat H_2 F_2$ ).

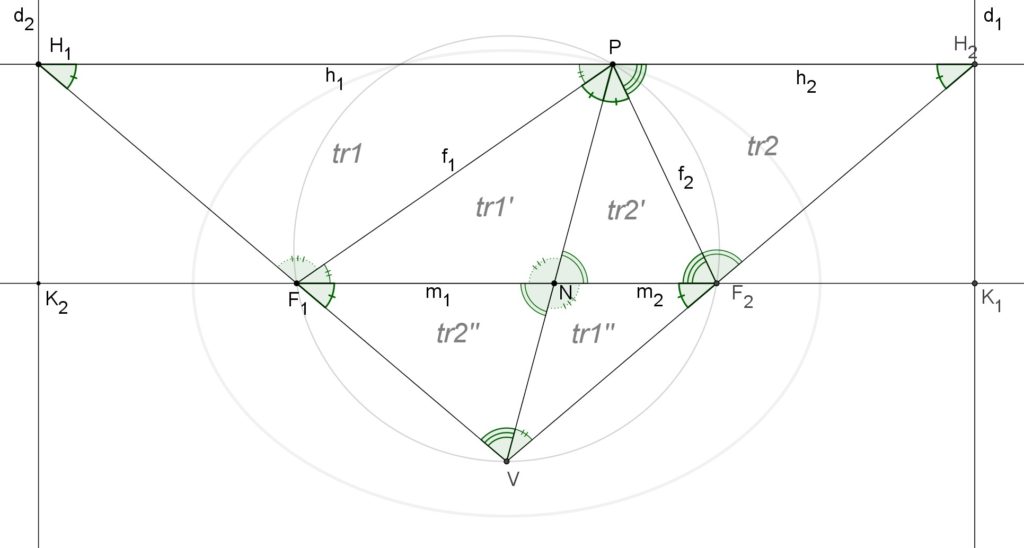
Here is an updated figure representing the geometric properties found so far, highlighting the similarity of the triangles $tr1,\;tr1',\;tr1''$ , the similarity of the triangles $tr2,\;tr2',\;tr2''$ and the congruent angles.

fig. 3: ellipse construction from focus-directrix (complete)

For the angle bisector theorem applied to the triangle $PF_1F_2$ , with the angle in $\widehat P$ bisected in the two congruent angles $F_1 \widehat{P} N$ and $N \widehat{P} F_2$ , it is

(a) $f_1:m_1=f_2:m_2$

For the similitude of the triangles $H_1PF_1$ and $PF_1N$ it is

(b) $m_1:f_1=f_1:h_1$

For the similitude of the triangles $H_2PF_2$ and $PF_2N$ it is

Putting together (a) with (b) and (c) it is

$f_1:h_1=f_2:h_2$

that is

$\overline{PF_1}/\overline{PH_1}= \overline{PF_2}/\overline{PH_2}=e$

Demonstration of II.2

Since

$f_1:d_1=f_2:d_2=e$

it follows that

$f_1=e\cdot d_1$

and

$f_2=e\cdot d_2$

Summing the terms it is

$f_1+f_2=e \cdot (d_1+d_2)=e \cdot \overline{H_1H_2}$

so that the sum of the distances of $P$ to the foci $F_1$ and $F_2$ has a constant value.
Q.E.D.

III) A geometric construction of the ellipse using definition B)

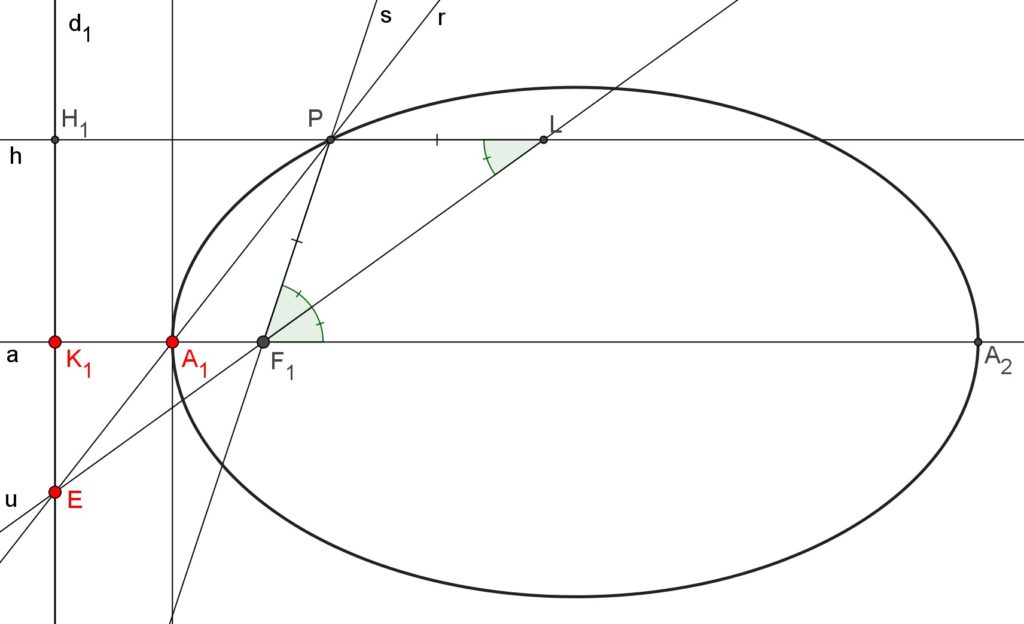
To enrich the geometrical investigation of the ellipse from the point of view of the definition B) here is a geometrical construction of the points $P$ of the ellipse.
It is based on the classic textbook
W. H. Besant – Conic Sections Treated Geometrically – 1895 – chapter 3 (see the References at the bottom for a link to the free ebook).
I’ve only changed the naming of the points and lines and have given some more detail to some of the passages.

With this construction, starting from a given directrix $d_1$ and a given focus $F_1$ and calling $H_1$ the perpendicular projection of $P$ on $d_1$ , each point $P$ of the ellipse must satisfy the condition

(d) $\overline{PF_1}/ \overline{PH_1}= \text{const}=e$

where $0<e<1$

fig. 4: geometric construction of the ellipse by W.H. Besant

Construction
Let $F_1$ be the focus, $d_1$ the directrix, $a$ the line through $F_1$ perpendicular to $d_1$ and $K_1$ the intersection between $a$ and $d_1$ .

Divide $F_1K_1$ at the point $A_1$ in the given ratio ( $\overline{F_1A_1}/\overline{A_1K_1}=e$ ).

The point $A_1$ is one point of the ellipse since it complies with the definition (d). In particular it is one of the ellipse vertices.
Construct another point $A_2$ on $a$ satisfying the proportion $\overline{F_1A_2}:\overline{K_1A_2}=\overline{F_1A_1}:\overline{K_1A_1}$ .
$A_2$ is another point of the ellipse and another of its vertices.

Choose some point $E$ anywhere on the directrix $d_1$ , join it with $F_1$ (line $u$ ) and draw, from $F_1$ another line $s$ such that it forms with the line $EF_1$ the same angle as the one that $EF_1$ forms with the horizontal line $a$ .
Join the points $E$ and $A_1$ to form the line $r$ and call $P$ the intersection point between the lines $s$ and $r$ .
Draw from $P$ a line $h$ parallel to the horizontal line $a$ . Call $H_1$ its intersection with the directrix $d_1$ and $L$ its intersection with the line $EF_1$ .
Since by construction it is $L\widehat{F_1}A_2=L\widehat{F_1}P$ and since $L\widehat{F_1}A_2N=P\widehat{L}F_1$ (alternate interior angles) it follows that $L\widehat{F_1}P=P\widehat{L}F_1$ and the triangle $PLF_1$ is isoceles.
Then it is $\overline{PL}=\overline{PF_1}$ .
Considering the parallel lines $h$ and $a$ , cut by the lines $r$ , $u$ and $d_1$ drawn from the common point $E$ , for Thales’ intercept theorem it is

$\overline{A_1F_1}:\overline{A_1K_1}=\overline{PL}:\overline{PH_1}=e$

and putting in the congruence between $\overline{PL}$ and $\overline{PF_1}$ it is also

$\overline{A_1F_1}:\overline{A_1K_1}=\overline{PF_1}:\overline{PH_1}=e$

Then the the point $P$ belongs to the locus of points (ellipse) for which it is $\overline{PF_1}:\overline{PH_1}=e= \text{const}$ .
Changing the choice of the point $E$ on $d_1$ will result in a different point $P$ but this will nonetheless belong to the same ellipse.

References

https://en.wikipedia.org/wiki/Ellipse
https://en.wikipedia.org/wiki/Dandelin_spheres
https://en.wikipedia.org/wiki/Conic_section
https://www.physicsforums.com/threads/ellipse-geometric-equivalence-of-two-definitions.247417/
W. H. Besant – Conic Sections Treated Geometrically (1895) – (free ebook in Project Gutenberg)

worlds of math & physics

Ellipse: geometric proof of the equivalence of two definitions

I) First part: A) $\rightarrow$ B)

II) Second part: B) $\rightarrow$ A)

III) A geometric construction of the ellipse using definition B)

References

Last edited 11 oct 2016

I) First part: A) B)

II) Second part: B) A)

III) A geometric construction of the ellipse using definition B)

References

Last edited 11 oct 2016

I) First part: A) $\rightarrow$ B)

II) Second part: B) $\rightarrow$ A)