Every time I try to get some deeper insight about Newton’s gravitational law I stumble upon the geometrical properties of the ellipse.
After many years of these strange and challenging encounters I really think that the ellipse is a rich and wonderful trove of geometrical nuances and subtleties…
Category Archives: Beautiful math
Mathematical flowers
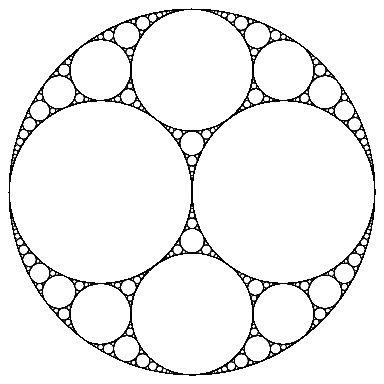
Apollonian gaskets: beautiful math can be simple
I’ve recently discovered the beauty, symmetry and mathematical richness of Apollonian gaskets.
Here’s a very short code (under 128 character’s length) that I’ve made with Wolfram Mathematica guided by the saying “Beautiful math can often also be very simple“.
Graphics[{Purple,Circle[],Disk@@@Flatten[Table[1/(k^2+2) {{(-1)^r (-k^2+1), -2 (-1)^j k},1}, {k,0,9}, {j,0,1}, {r,0,1}],2]}]
And here’s the twit published by @wolframtap (Wolfram Tweet-a-Program).
@sfera314 (More info: http://t.co/HBUuaZOB3w) #wolframlang pic.twitter.com/1aP7Wceob4
— Tweet-a-Program (@wolframtap) April 6, 2015
Well, actually that is not a complete Apollonian gasket, but it can give the idea.
To produce a full gasket the code should be longer than that allowed by a twitter length, but I think that a basic one could be done in about 500 characters or less.
Some links on Apollonian gaskets:
- https://en.wikipedia.org/wiki/Apollonian_gasket
- Apollonian_gasket A Tisket, a Tasket, an Apollonian Gasket (pdf), Dana Mackenzie, American Scientist, 2010
- The Circles of Descartes (Wolfram Demonstrations Project) – Contributed by: Ed Pegg Jr (you’ll need to have the Wolfram CDF Player installed to play with this full simulation)
Raindrops
Sometimes math can be completely useless, but amazingly simple and beautiful…
Another possible example of this fact is the following animation , that could be created with a very short code in Wolfram Mathematica (just 221 characters in total):
Animate[With[{r := RandomReal[]},
Graphics[BlockRandom[
Table[With[{z = r}, {, GrayLevel[2 (t - z)],
Thickness[0.03 (0.20 - t + z)],
Circle[{1.7 r, 0.82 r}, Max[0, t - z]]}], {k, 1, 45}]],
PlotRange -> {{0, 1.7}, {0, 0.82}}]],
{t, 0, 1}, DefaultDuration -> 20]
Too much long to be posted in in the twitter @wolframtap (Wolfram Tweet-a-Program). But short enough to show how some basic mathematical ideas can be very simple and yet beautiful (even if, maybe, useless). Here’s the video posted on youtube:
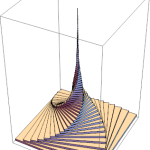
A twisted Eiffel tower (useless but beautiful math)
Sometimes math can be completely useless, but amazingly simple and beautiful.
A possible example of this is the following image, that could be created with a twitter-sized code in Wolfram Mathematica (123 characters in the present case):
Graphics3D[Table[Rotate[Cuboid[{-0.9^k, -0.9^k, (1/20)*k},
{0.9^k, 0.9^k, (1/20)*(k + 1)}], k*0.1, {0, 0, 1}], {k, 0, 60}]]
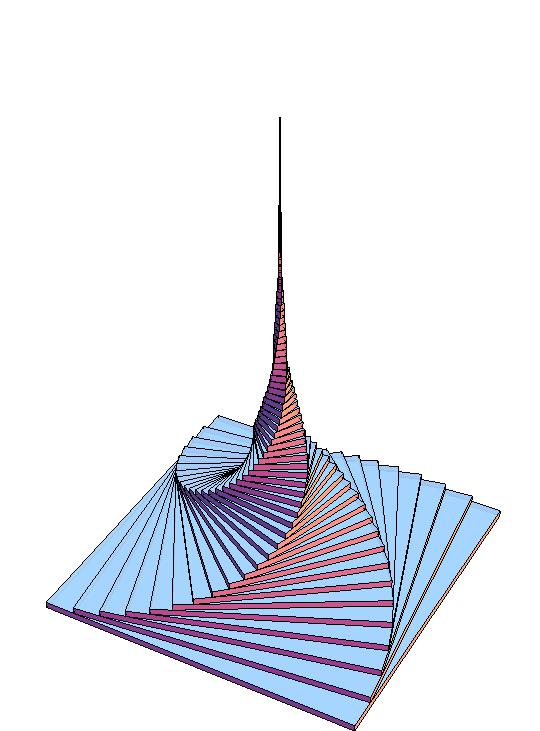 This mini-program was published (and favorited) in the twitter @wolframtap (Wolfram Tweet-a-Program).
This mini-program was published (and favorited) in the twitter @wolframtap (Wolfram Tweet-a-Program).
Here‘s the twit.
Another interesting thing about the fancy building depicted in the image is that, although it might have infinite height, it’ll still have a finite volume.
There’s also a small extension in this interactive demonstration (in which it’s possible to change the angle between consecutive parallelepipeds.
(Thanks to BV for suggesting me this beautiful idea)
 read more…
read more…