Author Archives: Luca M

Electric dance

Electric dance: a Coulombian 3-body problem with strong symmetries

I’m working on a simulation about a 3-body Coulombian system with very strong symmetries.

You can download the approved Mathematica code and/or the Wolfram CDF file at Wolfram Demonstration Project.

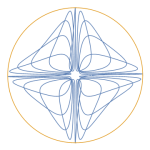
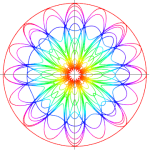
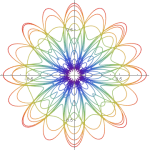
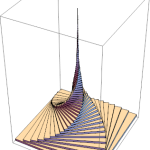
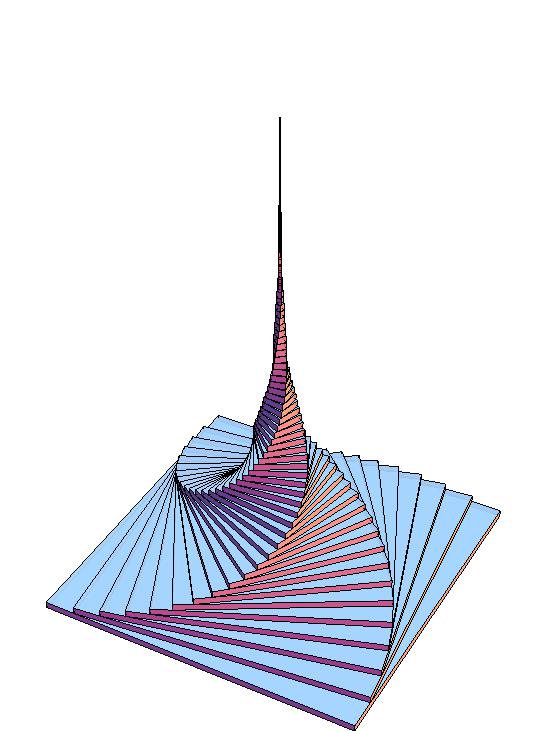
Three charged particles, two positive (blue) and one negative (red) are released from rest at the vertices of an isosceles triangle (equilateral in the initial setting).
It’s assumed that the particles have the same charge (but for the sign), the same mass (inertia) and that only the electric force acts on them.

The system dynamics will be just driven by Coulombian attractive/repulsive forces.
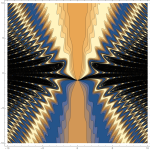
Anyway, given the strong symmetries in the initial conditions and given the conservation of energy and momentum, the system can be reduced to just a couple of differential equations, since the position/velocity of one of the blue particles is enough to set the positions/velocities of the other two. Here’s a video of the resulting “Electric dance”:


(YouTube link)

More info on this related page

First direct detection of gravitational waves by LIGO

In 1916, the year after the final formulation of the field equations of general relativity, Albert Einstein predicted the existence of gravitational waves.

Now, on 11 february 2016,  the detection of gravitational waves has been announced and the results have been published by Physical Review Letters.

The full article’s pdf from is available here

From

Phys. Rev. Lett. 116, 061102 – Published 11 February 2016

Abstract

Observation of Gravitational Waves from a Binary Black Hole Merger

On September 14, 2015 at 09:50:45 UTC the two detectors of the Laser Interferometer Gravitational-Wave Observatory simultaneously observed a transient gravitational-wave signal. The signal sweeps upwards in frequency from 35 to 250 Hz with a peak gravitational-wave strain of 1.0 \times {10^{ - 21}}. It matches the waveform predicted by general relativity for the inspiral and merger of a pair of black holes and the ringdown of the resulting single black hole. The signal was observed with a matched-filter signal-to-noise ratio of 24 and a false alarm rate estimated to be less than 1 event per 203 000 years, equivalent to a significance greater than 5.1σ. The source lies at a luminosity distance of 410_{ - 180}^{ + 160} Mpc corresponding to a redshift z=0.09_{ - 0.04}^{ + 0.03}. In the source frame, the initial black hole masses are 36_{ - 4}^{ + 5}M⊙ and 29_{-4}^{+4}M⊙, and the final black hole mass is 62_{-4}^{+4}M⊙, with 3.0_{-0.5}^{+0.5}M⊙{c^2} radiated in gravitational waves. All uncertainties define 90% credible intervals. These observations demonstrate the existence of binary stellar-mass black hole systems. This is the first direct detection of gravitational waves and the first observation of a binary black hole merger.

Apollonian gaskets: beautiful math can be simple

I’ve recently discovered the beauty, symmetry and mathematical richness of Apollonian gaskets.

Apollonian Gasket

An Apollonian Gasket of type -1_2_2_3

Here’s a very short code (under 128 character’s length) that I’ve made with Wolfram Mathematica guided by the saying “Beautiful math can often also be very simple“.

Graphics[{Purple,Circle[],Disk@@@Flatten[Table[1/(k^2+2) {{(-1)^r (-k^2+1), -2 (-1)^j k},1}, {k,0,9}, {j,0,1}, {r,0,1}],2]}]

And here’s the twit published by @wolframtap (Wolfram Tweet-a-Program).

Well, actually that is not a complete Apollonian gasket, but it can give the idea.
To produce a full gasket the code should be longer than that allowed by a twitter length, but I think that a basic one could be done in about 500 characters or less.

Some links on Apollonian gaskets:

An anticipatory interaction model for a crowd of pedestrians

A new interactive simulation created with the software Wolfram Mathematica, reproducing an anticipatory model for pedestrian interactions, is now available at this page of the CDF simulation section.

Here’s the demo video posted on youtube:

The model is based on the paper:

A universal power law governing pedestrian interactions
by Ioannis Karamouzas, Brian Skinner, and Stephen J. Guy

published on 2 December 2014 in Physical Review Letters

The article, together with some other interesting related material, is also available in this page  of the Applied Motion Lab, University of Minnesota.

The main point of the model is that the interaction force between two pedestrian is not based on their distance (as it’d happen for, say, electrons) but rather on their time-to-collision, which is defined as “the duration of time for which two pedestrians could continue walking at their current velocities before colliding”.

So, in this model you won’t see nearby pedestrians repel each other if their trajectories are not such to produce a collision in the next few seconds. That makes possible for pedestrians to walk side by side as it happens in the real world.
On the other hand two pedestrians about to collide will try to change their motion (in velocity direction and/or speed).
See the CDF simulations page for further details.

Phishing truths

A true story…

This is the text of an email message just received:

Dear customer,
Because of the numerous attempts of fraud suffered by our customers in the last 24 hours,
please check your account personal data in the link below.
www.popcredbank.com/blabla…..

Popular Credit Bank

But Popular Credit Bank is not my bank!

Yet they didn’t explicitly say that and they said the truth about the increasing number of recent attempts of fraud…

There’s some truth in a Liar that says “I’m a Liar”….

In the same way, there’s truth in a phishing message that starts by saying “since you are receiving phishing messages…”
Sort of a… Self-fulfilling prophecy

Raindrops

Sometimes math can be completely useless, but amazingly simple and beautiful…

Another possible example of this fact is the following animation , that could be created with a very short code in Wolfram Mathematica (just 221 characters in total):

Animate[With[{r := RandomReal[]}, 
  Graphics[BlockRandom[
    Table[With[{z = r}, {, GrayLevel[2 (t - z)], 
       Thickness[0.03 (0.20 - t + z)], 
       Circle[{1.7 r, 0.82 r}, Max[0, t - z]]}], {k, 1, 45}]], 
   PlotRange -> {{0, 1.7}, {0, 0.82}}]],
{t, 0, 1}, DefaultDuration -> 20]

Too much long to be posted in in the twitter @wolframtap (Wolfram Tweet-a-Program). But short enough to show how some basic mathematical ideas can be very simple and yet beautiful (even if, maybe, useless). Here’s the video posted on youtube:

A twisted Eiffel tower (useless but beautiful math)

Sometimes math can be completely useless, but amazingly simple and beautiful.
A possible example of this is the following image, that could be created with a twitter-sized code in Wolfram Mathematica (123 characters in the present case):

Graphics3D[Table[Rotate[Cuboid[{-0.9^k, -0.9^k, (1/20)*k}, 
{0.9^k, 0.9^k, (1/20)*(k + 1)}], k*0.1, {0, 0, 1}], {k, 0, 60}]]

EiffelThis mini-program was published (and favorited) in the twitter @wolframtap (Wolfram Tweet-a-Program).

Here‘s the twit.

Another interesting thing about the fancy building depicted in the image is that, although it might have infinite height, it’ll still have a finite volume.

There’s also a small extension in this interactive demonstration (in which it’s possible to change the angle between consecutive parallelepipeds.

(Thanks to BV for suggesting me this beautiful idea)