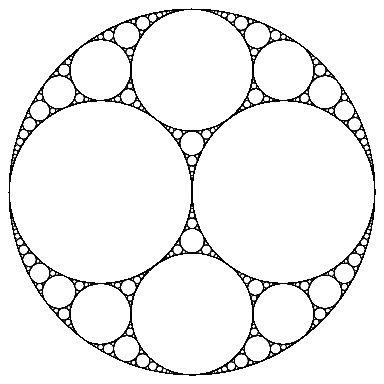
Apollonian gaskets: beautiful math can be simple

I’ve recently discovered the beauty, symmetry and mathematical richness of Apollonian gaskets.

Apollonian Gasket

An Apollonian Gasket of type -1_2_2_3

Here’s a very short code (under 128 character’s length) that I’ve made with Wolfram Mathematica guided by the saying “Beautiful math can often also be very simple“.

Graphics[{Purple,Circle[],Disk@@@Flatten[Table[1/(k^2+2) {{(-1)^r (-k^2+1), -2 (-1)^j k},1}, {k,0,9}, {j,0,1}, {r,0,1}],2]}]

And here’s the twit published by @wolframtap (Wolfram Tweet-a-Program).

Well, actually that is not a complete Apollonian gasket, but it can give the idea.
To produce a full gasket the code should be longer than that allowed by a twitter length, but I think that a basic one could be done in about 500 characters or less.

Some links on Apollonian gaskets: