There are deep and beautiful relationships between a function, its first derivative, its second derivative and its successive derivatives. A k derivative y-value reflect the rate of change of the k-1 derivative.
Here’s a demonstration trying to show that magic interplay between a function, its first derivative and its second derivative.
Monthly Archives: February 2014
The early universe as seen by the ESA’s Planck space telescope
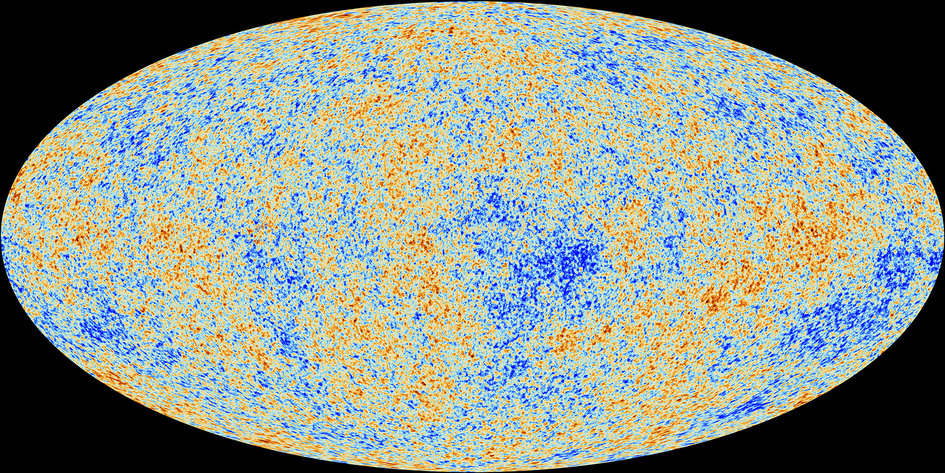
The anisotropies of the Cosmic microwave background (CMB) as observed by Planck. The CMB is a snapshot of the oldest light in our Universe, imprinted on the sky when the Universe was just 380 000 years old. It shows tiny temperature fluctuations that correspond to regions of slightly different densities, representing the seeds of all future structure: the stars and galaxies of today.
(Credits: ESA and the Planck Collaboration)
More info… (link to the ESA’s Planck project website)
The “dice roll with a given sum” problem
In some exercise taken from combinatorics textbooks you might find a question like: “if you roll 2 dice what is the probability to get 9 for the sum of the 2 dice faces?”
The answer is not much difficult and can be intuitively given by enumerating the number of cases that satisfy the given event and dividing that number with the number of all possible outcomes.
But what if you want to find the probability of, say, a sum of 31 when rolling 10 dice, where simple enumeration would require a very long time? Or to find a more general formula for the probability of getting p points as the sum of rolling n dice? Is there such a formula, computable without having to enumerate all the cases?
A nice (but not easy) combinatorics problem
Eight celebrities meet at a party. It so happens that each celebrity shakes hands with exactly two others. A fan makes a list of all unordered pairs of celebrities who shook hands with each other. If order does not matter, how many different lists are possible?
Annual Harvard-MIT Mathematics Tournament 2006