Category Archives: Math

math posts

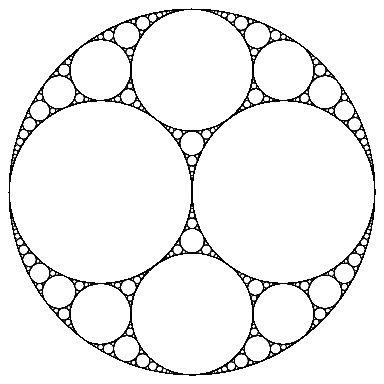
Apollonian gaskets: beautiful math can be simple

I’ve recently discovered the beauty, symmetry and mathematical richness of Apollonian gaskets.

Apollonian Gasket

An Apollonian Gasket of type -1_2_2_3

Here’s a very short code (under 128 character’s length) that I’ve made with Wolfram Mathematica guided by the saying “Beautiful math can often also be very simple“.

Graphics[{Purple,Circle[],Disk@@@Flatten[Table[1/(k^2+2) {{(-1)^r (-k^2+1), -2 (-1)^j k},1}, {k,0,9}, {j,0,1}, {r,0,1}],2]}]

And here’s the twit published by @wolframtap (Wolfram Tweet-a-Program).

Well, actually that is not a complete Apollonian gasket, but it can give the idea.
To produce a full gasket the code should be longer than that allowed by a twitter length, but I think that a basic one could be done in about 500 characters or less.

Some links on Apollonian gaskets:

Raindrops

Sometimes math can be completely useless, but amazingly simple and beautiful…

Another possible example of this fact is the following animation , that could be created with a very short code in Wolfram Mathematica (just 221 characters in total):

Animate[With[{r := RandomReal[]}, 
  Graphics[BlockRandom[
    Table[With[{z = r}, {, GrayLevel[2 (t - z)], 
       Thickness[0.03 (0.20 - t + z)], 
       Circle[{1.7 r, 0.82 r}, Max[0, t - z]]}], {k, 1, 45}]], 
   PlotRange -> {{0, 1.7}, {0, 0.82}}]],
{t, 0, 1}, DefaultDuration -> 20]

Too much long to be posted in in the twitter @wolframtap (Wolfram Tweet-a-Program). But short enough to show how some basic mathematical ideas can be very simple and yet beautiful (even if, maybe, useless). Here’s the video posted on youtube:

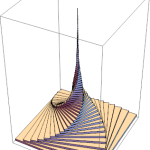
A twisted Eiffel tower (useless but beautiful math)

Sometimes math can be completely useless, but amazingly simple and beautiful.
A possible example of this is the following image, that could be created with a twitter-sized code in Wolfram Mathematica (123 characters in the present case):

Graphics3D[Table[Rotate[Cuboid[{-0.9^k, -0.9^k, (1/20)*k}, 
{0.9^k, 0.9^k, (1/20)*(k + 1)}], k*0.1, {0, 0, 1}], {k, 0, 60}]]

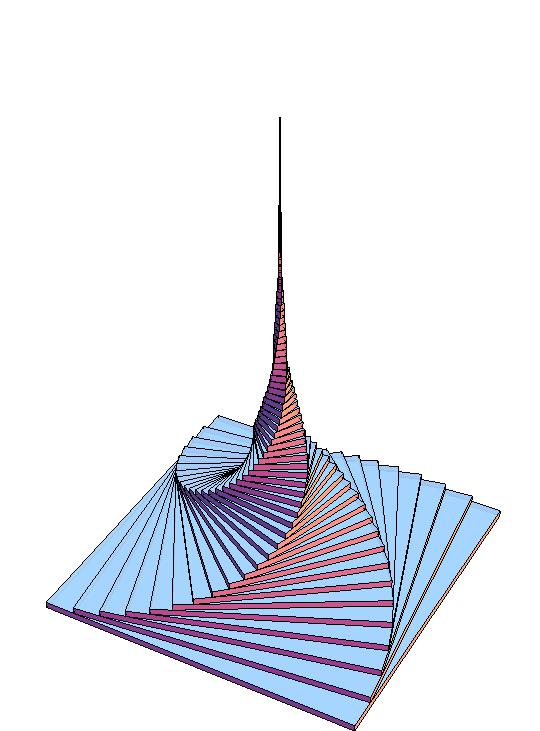EiffelThis mini-program was published (and favorited) in the twitter @wolframtap (Wolfram Tweet-a-Program).

Here‘s the twit.

Another interesting thing about the fancy building depicted in the image is that, although it might have infinite height, it’ll still have a finite volume.

There’s also a small extension in this interactive demonstration (in which it’s possible to change the angle between consecutive parallelepipeds.

(Thanks to BV for suggesting me this beautiful idea)

Waves propagation: the space view and the time view

It’s not easy to understand the mathematical inner workings of moving waves.
That’s because a wave is a perturbation in a media that changes with space and time.
So, even in the simplest case (i.e. waves propagating in a 1-dimensional media like a string) there are at least three variables involved: amount of the perturbation, position and time.

To understand better the relations between those variables and the wave parameters I’ve created, with the software Wolfram Mathematica, an interactive demonstration about moving waves. The demonstration has been exported in the .cdf format so that it can be interactively used with the free CDF Player (see here how to install it).

The CDF demonstration is available at this page.

It will show 4 different views;

• The moving wave
• The time view at a fixed position (x_0)
• The space view at fixed times (when the flash comes)
• The 3D view, in which there is also the moving point representing the state of the perturbation at x_0 as time goes by and its space-time trajectory.

In the demonstration it will be possible to change the wave parameters and see how its dynamic evolution changes accordingly.
For those who don’t have the free CDF Player installed on the PC (or those visiting this site from a a smartphone/tablet iOS/Android) here is a short video preview of the demonstration:

The mathematics of social networks: understanding the “six degrees of separation” theory

From: http://en.wikipedia.org/wiki/Six_degrees_of_separation

“Six degrees of separation is the theory that everyone and everything is six or fewer steps away, by way of introduction, from any other person in the world, so that a chain of “a friend of a friend” statements can be made to connect any two people in a maximum of six steps“

I’ve been intrigued by that theory and curious to investigate its mathematical basis.
A first step I took was to try to better understand the possible mathematical models aimed to reproduce the basic mechanisms about how the connections between people (or other abstract items ) can build up and develop.

Good sources for this quest were the following books:

  • Duncan J. Watts – Small Worlds: The Dynamics of Networks between Order and Randomness – [1999]
  • Steven Strogatz – Sync – [2003]

Here is a first personal investigation (made with Mathematica and exported as CDF) about Watts’ α-model:

Go to the demonstration’s page (in english)

Go to the demonstration’s page (in italian)

The “dice roll with a given sum” problem

In some exercise taken from combinatorics textbooks you might find a question like: “if you roll 2 dice what is the probability to get 9 for the sum of the 2 dice faces?”
The answer is not much difficult and can be intuitively given by enumerating the number of cases that satisfy the given event and dividing that number with the number of all possible outcomes.
But what if you want to find the probability of, say, a sum of 31 when rolling 10 dice, where simple enumeration would require a very long time? Or to find a more general formula for the probability of getting p points as the sum of rolling n dice? Is there such a formula, computable without having to enumerate all the cases?

Read full article…