[download as pdf: EMC2_rev01.pdf]
In this note we present the derivation of Einstein formula ![]() using the framework of classical dynamics with the addition of the expression for the relativistic momentum
using the framework of classical dynamics with the addition of the expression for the relativistic momentum ![]() .
.
A quick comparison is also made with the usual derivation of Newtonian kinetic energy.
We’ll consider a body with rest mass ![]() that starts from rest and reach the speed
that starts from rest and reach the speed ![]() . It’s energy is equal to the work done to make the body reach its final speed
. It’s energy is equal to the work done to make the body reach its final speed ![]() .
.
![]() since
since ![]()
In Newtonian mechanics, it is ![]() and, assuming the body’s mass doesn’t change, it is
and, assuming the body’s mass doesn’t change, it is
![]()
That’s the classical kinetic energy (KE) acquired by the body.
In relativity we must use a different expression for the momentum
![]() where
where ![]()
It can be noted that, in order to reconcile this new definition of momentum with the classic one (![]() ), it’s possible (even if a little controversial) to define the relativistic mass
), it’s possible (even if a little controversial) to define the relativistic mass ![]() as the mass of a moving body so that we can write
as the mass of a moving body so that we can write ![]()
In this case the integral is
![]()
We’ll calculate the integral in two different ways: a) with a substitution and using a trigonometric function for the ratio ![]() and b) without the substitution, keeping the original variables and following the usual rules for differentiation and integration.
and b) without the substitution, keeping the original variables and following the usual rules for differentiation and integration.
a) The “trig” route
The “trig” route presented in the following lines has some interesting geometric interpretations and makes the calculations easier. It’s based on a simple change of variable:
![]()
then ![]() and
and ![]()
meaning that ![]()
With these new expressions the integral becomes:
![]()
And the integration is almost straightforward:
![]()
Coming back to the original variables we have
![]()
So the relativistic kinetic energy is the excess of ![]() with respect to the invariant rest energy
with respect to the invariant rest energy ![]() and it is
and it is
![]()
Above equation leads to Einstein well-known formula ![]() when we define
when we define ![]() (total energy) as the sum of the kinetic energy (the energy due to the speed acquired) and the intrinsic rest energy (the base energy due to the rest mass only,
(total energy) as the sum of the kinetic energy (the energy due to the speed acquired) and the intrinsic rest energy (the base energy due to the rest mass only, ![]() ).
).
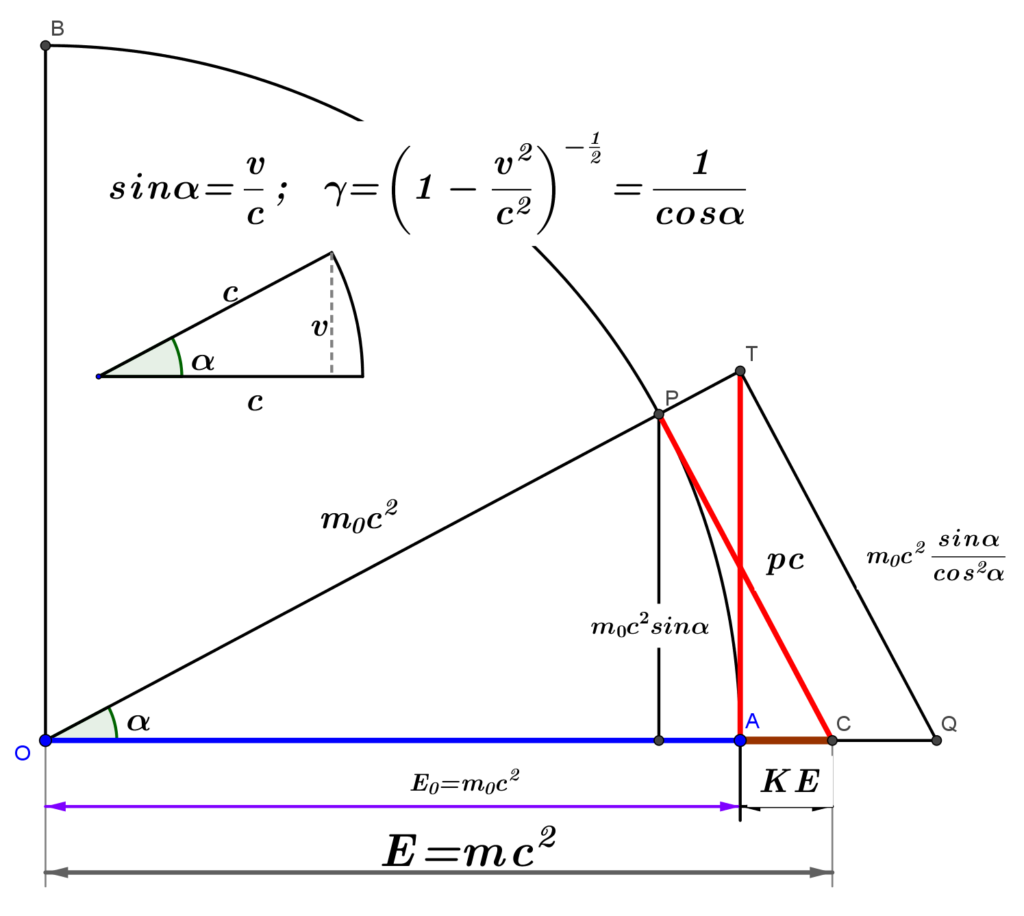
The following figure shows the interesting geometric relations between the main quantities involved in the derivation:
![]()
As a bonus we get the important energy-momentum relation
![]()
that follows from the simple application of Pythagoras’ theorem to the triangle ![]() .
.
b) Integration “as it is” and without substitution
We can also calculate the integral
![]()
without recurring to the previous substitution
Let’s first calculate the term ![]() :
:
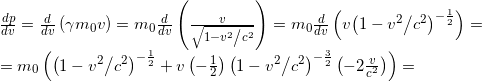
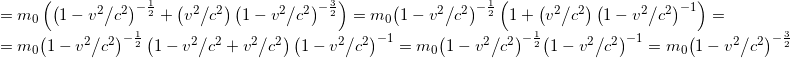
So it is
![Rendered by QuickLaTeX.com \[\begin{array}{l} W = \int {v\frac{{dp}}{{dv}}dv} = \int {v{m_0}{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \frac{3}{2}}}dv} = - \frac{{{m_0}{c^2}}}{2}\left( { - 2} \right)\left[ {{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \,\frac{1}{2}}}} \right]_0^v = \\ = {m_0}{c^2}\left( {{{\left( {1 - {{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {{c^2}}}} \right. \kern-\nulldelimiterspace} {{c^2}}}} \right)}^{ - \,\frac{1}{2}}} - 1} \right) = {m_0}{c^2}\left( {\gamma - 1} \right) = m{c^2} - {m_0}{c^2} \end{array}\]](https://www.lucamoroni.it/wp-content/ql-cache/quicklatex.com-89ebe765129e926c7535c664a0de4dab_l3.png)
We have reached the same result of the first calculation (with the “trig” substitution) but with some more effort and no evident geometric visualization and guidance.
Last updated: 1 june 2018