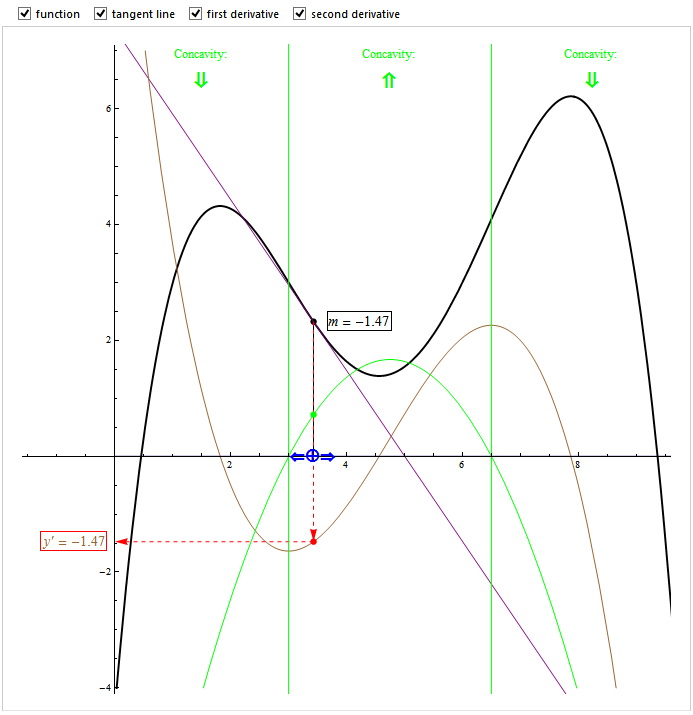
Answers:

• when the first derivative is positive the function is…
  increasing
• when the function is decreasing the first derivative is…
  negative
• when the first derivative crosses the x axis the function has…
  a horizontal tangent line and a change of behavior (from increasing to decreasing or from decreasing to increasing) , that is a local maximum or minimum. If the first derivative just touches the x-axis (without crossing it and so it’s tangent to the x-axis) then the function has an inflection point with a horizontal tangent line.
  
• when the function crosses the x axis the first derivative is…
  any… (the y-value of the derivative is just the slope of the function’s tangent line in the crossing point)
  
• when the function has a local maximum (or minimum) the first derivative…
  crosses the x-axis (it’s y-value is 0, that is )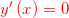
  
• when the first derivative has a local maximum (or minimum) the second derivative…
  crosses the x-axis (it’s y-value is 0, that is )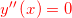
  
• when the function is concave upwards (smiling) its second derivative is…
  positive
  
• when the function is concave downwards (sad) its second derivative is…
  negative
  
• when the second derivative is zero the first derivative … and the function…
  the tangent line of the first derivative slope is zero and the function may have an inflection point.
  If the second derivative crosses the x-axis then first derivative has a local maximum or minimum and there’s actually an inflection point for the function.
  If the second derivative just touches the x-axis (without crossing it and so it’s tangent to the x-axis) then things are more complicated…
  
• when the second derivative is positive (negative) the first derivative …. and the function….
  the first derivative is increasing (decreasing) and the function has an upward (downward) concavity
  

[back to the Function derivatives demonstration]