The images presented in this page have been created with Wolfram Mathematica and posted on Wolfram’s Tweet-a-Program.
It’s not easy to create a tweet-length Wolfram Language program producing some interesting result. Sometimes that’s a real challenge.
The length of a tweet is 140 characters but, considering the need to put the address @wolframtap at the beginning of the text, the available characters are actually reduced to 128.
That’s a very short length!
So it’s really necessary to find some idea that can be “simple and beautiful” and then try to compress the code length as much as possible.
But the Beautiful Math can often be very concise, and simple enough to be reduced to a single tweet length.
Notes:
The image title links to the twit published by Tweet-a-Program.
The short Mathematica (Wolfram Language) code producing the image is written in the gray box just after the title.
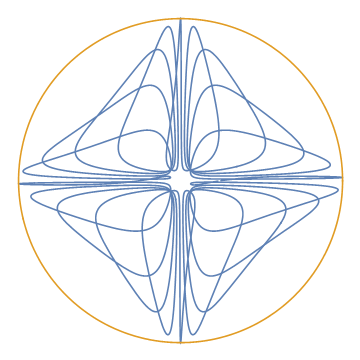
| Parametric paths |
ParametricPlot[{{Cos@t (4^(Sin[20 t]-1)),Sin@t (4^(Cos[20 t]-1))},{Cos@t, Sin@t}}, {t, 0, 6.28},Axes->False]
|
 |
| Rainbow flower |
a=.05;PolarPlot[4 a (Cos[4 t]^2 4^(2Sin[a t])+Sin[4 t]^2 4^(2Cos[a t]))^.5,{t,0,99},ColorFunction->(ColorData["Rainbow"][#4]&)]
|
 |
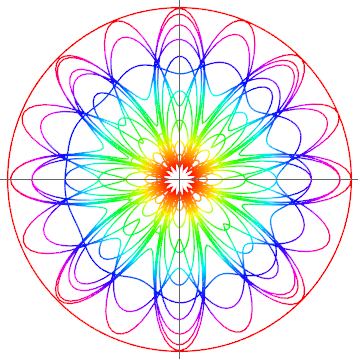
| Hue flower |
a=.05;PolarPlot[{5 a (Cos[4 t]^2 4^(2 Sin[a t])+Sin[4 t]^2 4^(2 Cos[a t]))^.5,1},{t,0,99},ColorFunction->(Hue[#4]&),Ticks->None]
|
 |
| Blue flower |
a={-2,2};f=1/4 E^Cos[16 t]-Sin[1/16 t];ParametricPlot[f {Sin[t],Cos[t]},{t,0,99},PlotRange->{a,a},PlotPoints->600,Axes->None]
|
 |
| Apollonian gasket |
Graphics[{Purple,Circle[],Disk@@@Flatten[Table[1/(k^2+2) {{(-1)^r (-k^2+1),-2 (-1)^j k},1},{k,0,9},{j,0,1},{r,0,1}],2]}]
|
 |
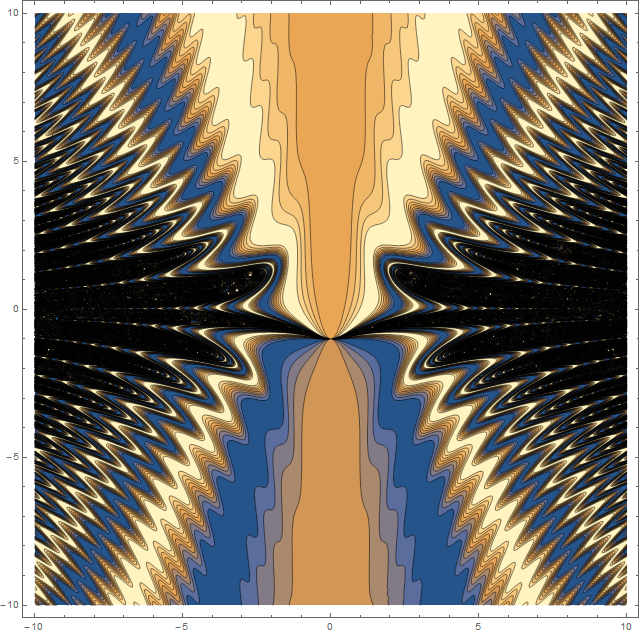
| Orion fires |
ContourPlot[Sin[x^2/(y+Cos[x y])],{x,-9,9},{y,-8,8},ImageSize->600,AspectRatio->0.6]
|
 |
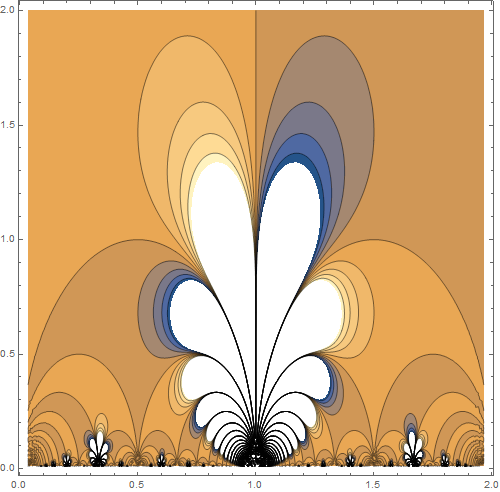
| Complex flora |
ContourPlot[Im[ModularLambda[(x+I 1/2 y)]],{x,0.035,1.965},{y,0.01,2},MaxRecursion->3,ImageSize->500]
|
 |
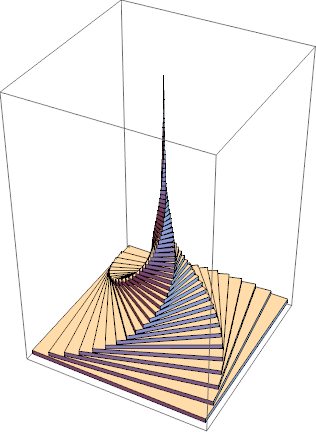
| Eiffel tower |
Graphics3D[Table[Rotate[Cuboid[{-0.9^k, -0.9^k, (1/20)*k}, {0.9^k, 0.9^k, (1/20)*(k + 1)}], k*0.1, {0, 0, 1}], {k, 0, 60}]]
|
 |