Come utilizzare le dimostrazioni CDF
scarica Watts_alpha_Model.cdf
scarica Watts_alpha_Model.nb (Mathematica notebook)
Note sulla simulazione
In questa dimostrazione, realizzata tramite il software Mathematica, viene riprodotto il modello ![]() di Duncan Watts, spiegato nel testo
di Duncan Watts, spiegato nel testo
Duncan J. Watts – Small Worlds: The Dynamics of Networks between Order and Randomness – [1999]
Il significato dei parametri del modello è il seguente:
![]() : numero totale di nodi della rete (o del grafo)
: numero totale di nodi della rete (o del grafo)
![]() : grado medio finale dei nodi della rete (numero medio di connessioni per i nodi della rete)
: grado medio finale dei nodi della rete (numero medio di connessioni per i nodi della rete)
![]() : parametro che permette di regolare il tipo di propensione dei nodi della rete a stabilire nuove connessioni. I due possibili estremi sono quello della comunità dei caveman (cavernicoli) con
: parametro che permette di regolare il tipo di propensione dei nodi della rete a stabilire nuove connessioni. I due possibili estremi sono quello della comunità dei caveman (cavernicoli) con ![]() e quello della comunità del pianeta solaria , con
e quello della comunità del pianeta solaria , con ![]() .
.
![]() : un valore di probabilità di base (tendenzialmente piccolo) per la creazione di una connessione casuale tra una qualsiasi coppia di nodi.
: un valore di probabilità di base (tendenzialmente piccolo) per la creazione di una connessione casuale tra una qualsiasi coppia di nodi.
Questo modello può essere utile per comprendere il funzionamento e lo sviluppo di una rete sociale (social network), partendo da un grafo iniziale che sia il più semplice possibile e che sia connesso (anello), e applicando una semplice regola del tipo “gli amici dei miei amici diventeranno probabilmente anche miei amici“.
Con valori diversi del parametro ![]() l’evoluzione della rete sarà guidata da una diversa propensione nella creazione di nuove connessioni: da quella in cui solo gli amici comuni determinano le nuove connessioni a quella in cui le nuove connessioni sono quasi esclusivamente casuali.
l’evoluzione della rete sarà guidata da una diversa propensione nella creazione di nuove connessioni: da quella in cui solo gli amici comuni determinano le nuove connessioni a quella in cui le nuove connessioni sono quasi esclusivamente casuali.
I coefficienti mean clustering coefficient e mean graph distance (calcolati nella dimostrazione) sono una misura della formazione di cluster (sottografi fortemente interconnessi) e della distanza media tra ogni coppia di nodi (lungo il cammino più breve) calcolata per tutte le coppie di nodi del grafo.
Secondo Watts le reti di tipo small worlds (piccoli mondi) sono caratterizzate contemporaneamente da un alto livello di aggregazione e da un basso grado di separazione.
Il testo di Watts illustra come sia possibile conciliare, per un certo intervallo di valori del parametro ![]() , questi due aspetti apparentemente contraddittori:
, questi due aspetti apparentemente contraddittori:
…nonostante ogni elemento tenda ad avere relazioni prevalentemente con pochi altri (alta aggregazione), ciò non impedisce di ottenere comunque una sua “vicinanza”, tramite pochi intermediari, con qualsiasi altro elemento della rete (basso grado di separazione).
[da wikipedia: Teoria del mondo piccolo]
Questo fenomeno è anche alla base della popolare teoria dei Sei gradi di separazione.
Uso della simulazione
Ogni modifica nei parametri globali della rete (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) innesca la necessità di ricalcolo dell’intera rete. Tale operazione può richiedere alcuni secondi di attesa per valori relativamente grandi di
) innesca la necessità di ricalcolo dell’intera rete. Tale operazione può richiedere alcuni secondi di attesa per valori relativamente grandi di ![]() e/o
e/o ![]() .
.
Il parametro t, invece mostra solo i passaggi che hanno portato alla costruzione della rete, fino al raggiungimento del suo livello finale di connessione, e non necessita quindi di un ricalcolo dell’intera rete (ed è molto più veloce).
Il modello
Il fondamento logico del modello ![]() e la funzione svolta dai suoi parametri (
e la funzione svolta dai suoi parametri (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) sono spiegati nel testo;
) sono spiegati nel testo;
Duncan J. Watts – Small Worlds: The Dynamics of Networks between Order and Randomness
[Princeton University Press – 1999]
Tramite il sito Google Books è (al momento) possibile visualizzare alcuni estratti del testo sopracitato (in inglese) tra cui proprio la parte in cui viene spiegato il significato dei parametri e il meccanismo di funzionamento del modello (da pag.44 a pag. 48). Cliccare qui e poi selezionare il link per la pagina 46.
I parametri usati dal modello sono:
![]() : numero totale di nodi della rete (o del grafo).
: numero totale di nodi della rete (o del grafo).
![]() : numero medio di connessioni per ogni nodo (o numero medio di amici per ogni membro della comunità). Tale valore sarà raggiunto solo al termine del processo di costruzione della rete. I parametri
: numero medio di connessioni per ogni nodo (o numero medio di amici per ogni membro della comunità). Tale valore sarà raggiunto solo al termine del processo di costruzione della rete. I parametri ![]() and
and ![]() determinano il numero finale di connessioni del grafo:
determinano il numero finale di connessioni del grafo: ![]() .
.
Un grafo completo (o totalmente connesso) è un grafo in cui ogni nodo è collegato direttamente a tutti gli altri nodi e questo tipo di grafo ha il massimo valore di ![]() per un dato valore di
per un dato valore di ![]() , con
, con ![]() e
e ![]()
![]() (
(![]() ) è un parametro in grado di regolare il tipo di propensione dei nodi della rete a stabilire nuove connessioni, tra la tipologia caveman (
) è un parametro in grado di regolare il tipo di propensione dei nodi della rete a stabilire nuove connessioni, tra la tipologia caveman (![]() ) a quella solaria (
) a quella solaria (![]() ).
).
La comunità caveman tende a stabilire nuove connessioni solo tra gli abitanti della stessa caverna, in modo che, ad esempio, tutti i membri della caverna A formeranno facilmente legami tra loro e costituiranno un gruppo altamente interconnesso (cluster) di amici. La stessa cosa succederà per un’altra caverna B.
Allo stesso tempo, però, ci sarà una bassa probabilità che un abitante della caverna A possa essere connesso con un abitante della caverna B. Questa tipologia di relazione sociale può essere descritta dalla frase “Ogni persona che conosco conosce tutte le altre persone che conosco e nessun’altra persona (o quasi)“.
All’estremo opposto si trova la comunità solaria. I suoi membri potrebbero essere paragonati ai moderni utenti di chat-room che possono entrare in contatto, in modo altamente casuale, con qualsiasi altro essere umano (e non prevalentemente con gli amici degli amici). In questa comunità le amicizie già consolidate non hanno praticamente alcun effetto nella creazione di nuove amicizie e le nuove relazioni sono principalmente governate dal caso.
![]() (
(![]() ) è un valore di probabilità di base per la creazione di una connessione casuale tra una qualsiasi coppia di nodi. In questo modello
) è un valore di probabilità di base per la creazione di una connessione casuale tra una qualsiasi coppia di nodi. In questo modello ![]() deve avere un valore molto basso (ad es. 0.001 o anche molto meno per reti più grandi) per non oscurare il ruolo del parametro
deve avere un valore molto basso (ad es. 0.001 o anche molto meno per reti più grandi) per non oscurare il ruolo del parametro ![]() . Questo parametro acquista rilevanza solamente nei casi in cui il valore di
. Questo parametro acquista rilevanza solamente nei casi in cui il valore di ![]() renda il numero di amici comuni tra due nodi irrilevante per la creazione di una nuova connessione.
renda il numero di amici comuni tra due nodi irrilevante per la creazione di una nuova connessione.
Il modello ![]() di Duncan Watts è basato sul seguente algoritmo ciclico:
di Duncan Watts è basato sul seguente algoritmo ciclico:
1. Al passo (tempo) ![]() viene analizzato il grafo costruito al termine del passo precedente
viene analizzato il grafo costruito al termine del passo precedente ![]() e, per ogni coppia di nodi
e, per ogni coppia di nodi ![]() e
e ![]() (che non sono già connessi) vengono calcolati:
(che non sono già connessi) vengono calcolati:
• ![]() : numero di nodi adiacenti ad entrambi i nodi
: numero di nodi adiacenti ad entrambi i nodi ![]() and
and ![]() (amici comuni di i e j)
(amici comuni di i e j)
• ![]() : grado medio del grafo al tempo
: grado medio del grafo al tempo ![]() , cioè numero medio di connessioni (amici) per i nodi della rete al tempo
, cioè numero medio di connessioni (amici) per i nodi della rete al tempo ![]() .
.
2. Viene poi calcolata la matrice di propensità ![]() in base alla seguente formula:
in base alla seguente formula:
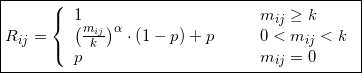
La matrice di propensità ![]() viene poi normalizzata per ottenere una matrice di probabilità
viene poi normalizzata per ottenere una matrice di probabilità ![]() , con
, con 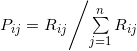 tale che
tale che ![]() .
.
In questa matrice ![]() assume il valore della probabilità della connessione che il nodo i possa connettersi con il nodo j.
assume il valore della probabilità della connessione che il nodo i possa connettersi con il nodo j.
La regola sopracitata per il calcolo della matrice ![]() si traduce nei seguenti due casi estremi.
si traduce nei seguenti due casi estremi.
Per le comunità pure di tipo caveman (![]() ) si avrà:
) si avrà:
![]() .
.
Questo significa che due persone con anche un solo amico in comune avranno una probabilità molto maggiore di stabilire una connessione rispetto a due persone senza alcun amico in comune (dato che ![]() è piccolo).
è piccolo).
All’altro estremo, per le comunità pure di tipo solaria (![]() ) si avrà:
) si avrà:
![]() .
.
Questo significa che, a meno che i nodi i e j abbiano raggiunto una soglia critica di amici comuni, la probabilità della loro connessione sarà la stessa di una analoga coppia di nodi del tutto privi di amici comuni.
Nel modello di Watts, la soglia critica per il numero di amici comuni che può far scattare la connessione (in un mondo dove gli amici comuni contano poco), è impostata ad un livello piuttosto elevato che corrisponde al livello medio di interconnessioni per ogni nodo della rete. Questa scelta può essere interpretata considerando che, anche in una comunità di tipo solaria, se due persone non connesse hanno tutti i loro amici in comune (e questo è abbastanza improbabile dato che ci si può aspettare che i nodi i e j abbiano diversi altri amici non in comune) allora non potranno davvero evitare che si stabilisca un contatto anche tra loro.
Le forme intermedie tra i due opposti estremi delle comunità di tipo caveman e solaria sono più verosimili per interpretare ciò che succede nel mondo reale.
La seguente figura mostra la relazione esistente tra la la propensione a stabilire un collegamento (“propensity to become friends”) e il rapporto tra amici in comune e numero totale di amici (“mutual friends as a fraction of total friends“) per differenti possibili valori del parametro ![]() .
.
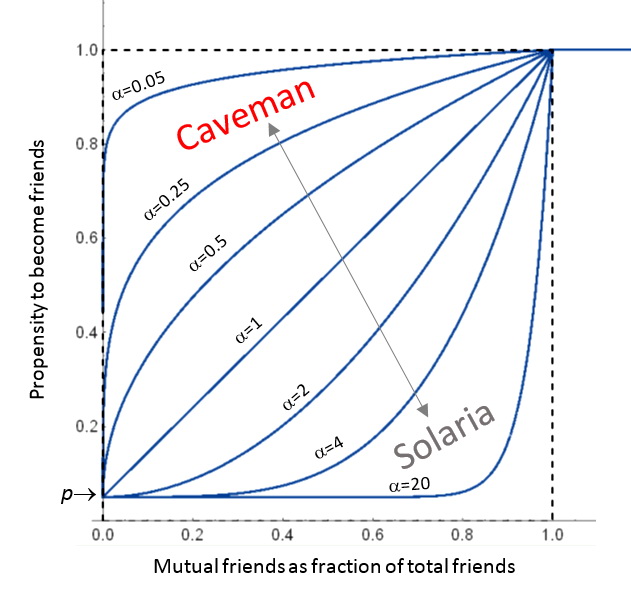 Il modello α è una variante del più conosciuto (e più semplice) modello β (anche chiamato Watts–Strogatz model). Rispetto a quest’ultimo, Il modello α è, comunque, potenzialmente più ricco e interessante per le sue specifiche caratteristiche dinamiche, che possono aiutare a comprendere meglio e a visualizzare l’evoluzione e lo sviluppo di una rete sociale.
Il modello α è una variante del più conosciuto (e più semplice) modello β (anche chiamato Watts–Strogatz model). Rispetto a quest’ultimo, Il modello α è, comunque, potenzialmente più ricco e interessante per le sue specifiche caratteristiche dinamiche, che possono aiutare a comprendere meglio e a visualizzare l’evoluzione e lo sviluppo di una rete sociale.
L’algoritmo
Il meccanismo per la costruzione del grafo finale è basato su un ciclo iterativo.
In ogni blocco del ciclo viene generata una nuova connessione per la rete e il ciclo termina quando viene raggiunto il numero ![]() finale di connessioni:
finale di connessioni: ![]() .
.
La condizione iniziale del grafo è un anello topologico (topological ring) in cui ogni nodo è connesso ai soli due nodi adiacenti (due soli amici per ogni individuo: l’amico di destra e quello di sinistra), formando un unico percorso continuo tra nodi interconnessi.
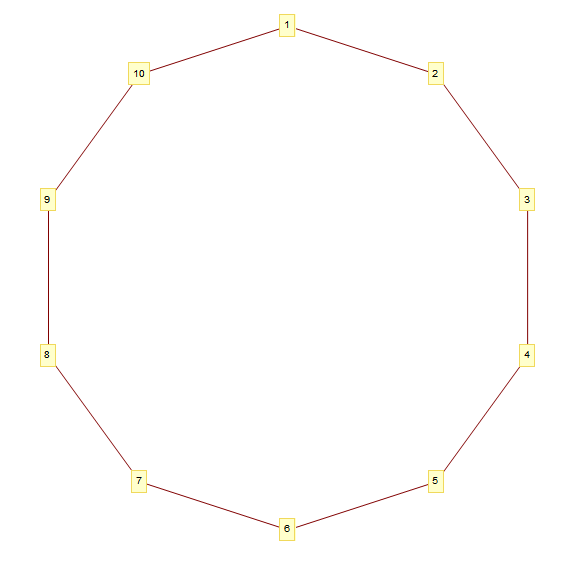 Dopo questa condizione iniziale la rete si sviluppa con una combinazione di fattori deterministici e stocastici. Questi ultimi sono regolati dai parametri
Dopo questa condizione iniziale la rete si sviluppa con una combinazione di fattori deterministici e stocastici. Questi ultimi sono regolati dai parametri ![]() e
e ![]() che determinano il grado probabilistico insito nell’assunzione “l’amico del mio amico diventerà presto, con una certa probabilità, anche mio amico“.
che determinano il grado probabilistico insito nell’assunzione “l’amico del mio amico diventerà presto, con una certa probabilità, anche mio amico“.
Il processo di costruzione della rete continua in questo modo sino a raggiungere il previsto livello medio di connessioni (amici) per ogni nodo (persona). Questo numero medio di connessioni è espresso dal parametro ![]() .
.
Nota: la scelta di una specifica e particolare condizione iniziale può sembrare arbitraria ed avere qualche influenza non desiderata sulla successiva evoluzione della rete ma è comunque motivata dalle seguenti considerazioni:
• Il grafo iniziale è connesso (nel senso che ogni nodo è raggiungibile da ogni altro nodo) e rimarrà connesso anche nel corso della sua successiva evoluzione, dato che l’algoritmo aggiunge un nuovo collegamento in ogni passaggio ma non elimina mai collegamenti esistenti.
Questo fatto rende possibile il calcolo della distanza media tra due nodi qualsiasi del grafo ed evita il caso di un grafo che mantenga, anche al termine del processo di costruzione, sottografi disconnessi tra loro (isole).
Questa eventualità è possibile in alcune reti sociali e sicuramente questa era una situazione tipica nelle reti sociali del mondo del passato, ma ciò non rifletterebbe adeguatamente la caratteristica di quasi totale interconnessione del mondo digitale contemporaneo.
• Ha una struttura minima: nessun nodo è speciale o privilegiato (come avverrebbe, ad esempio, in una struttura a stella) o differente da ogni altro nodo in per numero di connessioni con gli altri nodi.
• È minimamente connesso, dato che possiede il minimo numero di collegamenti rispetto a tutti gli altri possibili grafi connessi aventi una struttura minima.
Duncan J. Watts chiama questa condizione iniziale un substrato e spiega come la scelta di un grafo ad anello come substrato (rispetto ad altre scelte) sia quella destinata ad avere il minimo impatto sulla successiva evoluzione del grafo finale, anche considerando le caratteristiche di interdipendenza delle reti sociali moderne che il modello dovrebbe riprodurre.
Dato che la condizione iniziale è un grafo con ![]() nodi e
nodi e ![]() connessioni, e dato che ogni iterazione del ciclo aggiunge al grafo una connessione, per raggiungere il numero finale di connessioni (
connessioni, e dato che ogni iterazione del ciclo aggiunge al grafo una connessione, per raggiungere il numero finale di connessioni (![]() ) saranno necessarie
) saranno necessarie ![]() iterazioni.
iterazioni.
Nella generica t-esima iterazione del ciclo saranno effettuate le seguenti operazioni:
• Scelta semi-casuale (vedi sotto) di un nodo i.
• Per ogni altro nodo j, vengono calcolate le matrici ![]() e
e ![]() .
.
Gli elementi di queste due matrici dipendono non solo dai valori dei parametri generali del modello (![]() e
e ![]() ) ma anche dai valori assunti dalla matrice
) ma anche dai valori assunti dalla matrice ![]() e dalla variabile
e dalla variabile ![]() che sono calcolati a partire dalla matrice di adiacenza calcolata al termine della precedente iterazione
che sono calcolati a partire dalla matrice di adiacenza calcolata al termine della precedente iterazione ![]() .
.
• Il nodo i viene quindi connesso con un altro nodo j. La scelta è casuale ma ponderata dalle probabilità contenute nella matrice ![]() .
.
• Essendo stata creata la nuova connessione tra i e j ci sarà l’aggiornamento della matrice di adiacenza (simmetrica) che conterrà quindi un nuovo 1 nelle posizioni ij e ji.
I nodi i sono scelti in ordine casuale, ma dopo che un certo nodo è stato prescelto, e avrà quindi avuto la possibilità di scegliere un nuovo vicino (j), non potrà più scegliere ancora fino a quando tutti gli altri nodi avranno avuto, a turno, la stessa opportunità.
Questa democratica procedura limita la possibilità che un nodo possa essere selezionato più frequentemente di altri per assumere il ruolo di decisore del proprio nuovo amico, ma non impedisce comunque la possibilità che qualche nodo (più carismatico) venga scelto (dagli altri nodi) più frequentemente di altri nodi.
Ciò implica che il grado di connessione ![]() dei singoli nodi assumerà verosimilmente, nel corso del processo di costruzione della rete, valori differenziati per i diversi nodi e che qualche nodo potrà quindi assumere il ruolo di catalizzatore per la formazione di cluster locali.
dei singoli nodi assumerà verosimilmente, nel corso del processo di costruzione della rete, valori differenziati per i diversi nodi e che qualche nodo potrà quindi assumere il ruolo di catalizzatore per la formazione di cluster locali.
I nodi carismatici saranno caratterizzati da un grado ![]() più elevato del grado medio dei nodi della rete.
più elevato del grado medio dei nodi della rete.
D’altra parte i nodi meno carismatici avranno comunque il loro turno nella scelta di nuovi amici e potranno comunque, sebbene più lentamente, aumentare il loro numero di amici (da 2 a un minimo valore finale di ![]() , nel caso estremo in cui non vengano mai scelti da altri nodi).
, nel caso estremo in cui non vengano mai scelti da altri nodi).
Considerazioni finali
La congettura di Watts è espressa dal seguente enunciato:
Esiste una tipologia di grafi che sono caratterizzati da una forte clusterizzazione ma che, allo stesso tempo, mostrano una distanza media ridotta e proprietà di scala simili a quella di grafi casuali. Questi grafi sono chiamati grafi del mondo piccolo.
[There exist a class of graphs that are highly clustered yet have characteristic length and length scaling properties equivalent to random graphs. These are called small-world graphs. (p.58)]
Per verificare tale congettura Watts ha utilizzato il suo modello ![]() per produrre simulazioni numeriche. Tali simulazioni hanno confermato la molto probabile veridicità della congettura.
per produrre simulazioni numeriche. Tali simulazioni hanno confermato la molto probabile veridicità della congettura.
La dimostrazione presentata in questa pagina, che replica il modello ![]() su piccola scala, è troppo limitata nel numero di nodi della rete che può gestire e non è pertanto del tutto adatta a fornire un ulteriore strumento di verifica della congettura sopra citata. La restrizione sul valore di
su piccola scala, è troppo limitata nel numero di nodi della rete che può gestire e non è pertanto del tutto adatta a fornire un ulteriore strumento di verifica della congettura sopra citata. La restrizione sul valore di ![]() è necessaria per contenere i tempi di ricalcolo della rete entro livelli accettabili per una simulazione interattiva.
è necessaria per contenere i tempi di ricalcolo della rete entro livelli accettabili per una simulazione interattiva.
Malgrado questo limite la dimostrazione può comunque essere utile per avere una migliore comprensione dei meccanismi che sono alla base del modello ![]() e per meglio intuire le possibili dinamiche che portano all’insorgenza di reti del mondo piccolo (small-world networks) nella realtà sociale contemporanea.
e per meglio intuire le possibili dinamiche che portano all’insorgenza di reti del mondo piccolo (small-world networks) nella realtà sociale contemporanea.
Riferimenti
da it.wikipedia.org:
Teoria del mondo piccolo
Sei gradi di separazione
Teoria dei grafi
Grafo
Glossario di teoria dei grafi
da altri siti:
Teoria delle reti e “piccoli mondi”. Sguardo d’insieme alla network analysis e breve storia di un’idea
La teoria delle reti negli studi genomici (tesi di laurea di Cinzia Moretti)
I “gradi di separazione” su Facebook
altri riferimenti (in inglese):
♦ da http://en.wikipedia.org:
Graph theory, Six degrees of separation, Small-world network
♦ da http://www.youtube.com:
The Science of Six Degrees of Separation
Un video del grande Veritasium che spiega i principi basilari della teoria dei “Sei gradi” (si possono visualizzare i sottitotioli in inglese).
♦ da altri siti:
Reka Albert, Albert-Laszlo Barabasi: Statistical mechanics of complex networks (pdf – arxiv.org)
Duncan J. Watts, Steven H. Strogatz: Collective dynamics of ‘small-world’ networks (pdf – Nature 393, 440-442 – 4 June 1998)
The story of networks (blog – http://www.digitaltonto.com)
David Easley, Jon Kleinberg: Networks, Crowds, and Markets: Reasoning About a Highly Connected World – Cambridge University Press – 2010. There is a complete pre-publication draft (pdf) downloadable at above authors’ page.
♦ libri:
Duncan J. Watts – Small Worlds: The Dynamics of Networks between Order and Randomness – Princeton University Press – 1999
Steven Strogatz – Sync – Penguin Books – 2003
Autore: Luca Moroni – Ottobre 2014